Wechselstrom und Wechselspannung

Tesla ist der Endecker von Wechselstrom und Drehstrom. Beide haben schnell weltweite Anwendung gefunden. Ohne diese Entdeckung von Tesla, die es erst möglich machte, elektrischen Strom über viele Hunderte von Kilometern zu übertragen, gäbe es die heutige Selbstverständlichkeit der Elektrizität mit ihren enorm vielseitigen Anwendungen nicht.

Bei Wechselstrom und Wechselspannung spricht man von elektrischen Größen, die in den Einheiten Ampere (A) und Volt (V) angegeben werden, deren Werte sich im Verlauf der Zeit (t) regelmäßig wiederholen. Der Wechselstrom ist ein elektrischer Strom, der periodisch seine Polarität (Richtung) und seinen Wert (Stromstärke) ändert. Das selbe gilt für die Wechselspannung.
Es gibt verschiedene Arten von Wechselstrom. Reine Wechselgrößen sind die Rechteckspannung, die Sägezahnspannung, die Dreieckspannung und die Sinusspannung (Welle) oder eine Mischung aus allen diesen Varianten.
In der Elektrotechnik werden hauptsächlich Wechselspannungen mit sinusförmigem Verlauf verwendet. Beim sinusförmigen Kurvenverlauf treten die geringsten Verluste und Verzerrungen auf. Deshalb werden die folgenden Beschreibungen des Wechselstromes und der Wechselspannung anhand des sinusförmigen Kurvenverlaufs erklärt.
Wechselspannung wird durch Generatoren in Kraftwerken erzeugt. Dabei dreht sich ein Roter im Generator um 360 Grad. Dadurch entsteht eine Spannung mit wechselnder Polarität, also ein sinusförmiger Verlauf.
Die wichtigste Wechselspannung ist 230 Volt aus unserem Stromnetz. Es hat eine Frequenz von 50 Hz. Das sind 50 Umdrehungen in der Sekunde eines Rotors im Generator.

Kennwerte der Sinusspannung

• Augenblickswert und Amplitude
• Periode und Frequenz

Augenblickswert und Amplitude

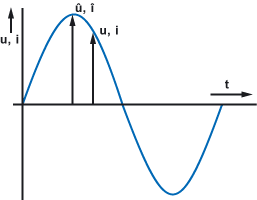
Da eine Wechselspannung nie einen konstanten Spannungswert hat, spricht man bei elektrischen Wechselgrößen, deren Zeitabhängigkeit gezeigt werden soll, von Augenblickswerten (Momentanwerte). Diese Augenblickswerte werden durch einen Kleinbuchstaben (Formelzeichen) angegeben.
Maximal- bzw. Scheitelwerte der Amplitude von sinusförmigen zeitabhängigen Wechselgrößen werden durch ein Dach über dem Formelzeichen gekennzeichnet. Beispiele dazu wären die Spannung û (sprich: u-Dach) und der Strom î (sprich: i-Dach).
Bei bekanntem Scheitelwert lässt sich bei jedem beliebigen Drehwinkel λ ( = 0° ... 360°) der Augenblickswert berechnen.

Periode und Frequenz

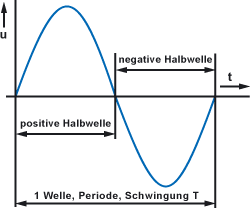
Die positive und die negative Halbwelle einer Schwingung bezeichnet man als Periode. Die Zeit die zum Durchlaufen der Periode benötigt wird ist die Periodendauer Τ. Die Periodendauer Τ wird in Sekunden angegeben.
Die Frequenz gibt die Zahl der Perioden an, die in einer Sekunde durchlaufen werden. Die Frequenz wird in Hertz (Hz) angegeben.
Die Frequenz ist der Kehrwert der Periodendauer. Das bedeutet, die Frequenz ist um so größer, je kleiner die Periodendauer ist.

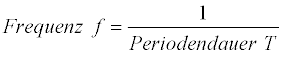
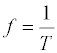
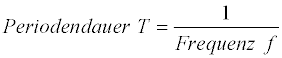
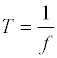
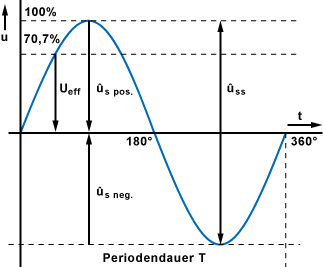
Kennwerte einer Sinuskurve

Formelzeichen	Beschreibung	Formel
ûss	Die Spitze-Spitze-Spannung ûss liegt zwischen dem positiven und negativen Spitzenwert einer Periodendauer.
ûs	Die Spitze-Spannung ûs ist das positive oder das negative Maximum einer Halbwelle.
Ueff	Der Effektivwert Ueff ist ca. 70,7% der Spitze-Spannung ûs. Wechselspannungswerte werden in der Regel als Effektivwert angegeben. Ein Wechselstrom von 1 A (Effektivwert) bewirkt dieselbe Wärmeleistung in einem Widerstand wie ein Gleichstrom von 1 A. Der Effektivwert ist wie der Gleichrichtwert ein Mittelwert und ist daher mit einem Großbuchstaben als Formelzeichen zu bezeichnen.
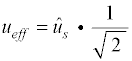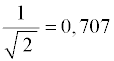T	Die Periodendauer T ist die Dauer eines periodischen Schwingungsverlaufs.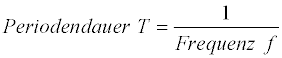
f	Die Frequenz f gibt die Anzahl der Schwingungen pro Sekunde an.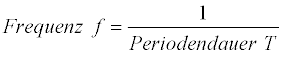