Digitale Signatur
Die digitale bzw. elektronische Signatur ist eine schlüsselabhängige Prüfsumme, die von einer Nachricht oder einem Dokument in Kombination mit einem Schlüssel erzeugt wird. Wird die Signatur an eine Nachricht oder ein Dokument angehängt, dann gilt das als unterschrieben. Für digitale Nachrichten und Dokumente werden digitale Signaturen verwendet, um ihre Echtheit glaubhaft und prüfbar zu machen. Die Echtheit der Signatur kann elektronisch geprüft werden.
Digitale Signaturen sind in der Datenübertragung deshalb notwendig, weil sich der Absender von Nachrichten und Dokumenten fälschen lässt. Beispielsweise ist es ganz einfach den Absender einer E-Mail zu fälschen. Das heißt, es ist möglich, dass sich jemand als eine andere Person ausgibt. Auch im wirklichen Leben kann man eine beliebige Absender-Adresse auf einen Brief schreiben. Um die Glaubwürdigkeit des Briefs zu unterstreichen setzen wir an das Briefende unsere Unterschrift. Genauso wird es mit der digitalen Signatur gemacht.
Für digitale Signaturen gelten folgende Anforderungen:
- Die digitale Signatur darf nicht (unbemerkt) fälschbar sein.
- Die Echtheit der digitalen Signatur muss überprüfbar sein.
- Die digitale Signatur darf nicht von einem Dokument auf ein anderes (unbemerkt) übertragbar sein.
- Das signierte Dokument darf nicht (unbemerkt) veränderbar sein.
Eine Infrastruktur mit digitalen Signaturen macht nur dann Sinn, wenn die Signaturen in übertragenen Nachrichten und Dokumenten ständig geprüft werden. Nur dann kann erkannt werden, wenn eine Signatur, eine Nachricht oder ein Dokument gefälscht wurde. Wenn die Prüfung nicht erfolgt, dann bleiben Manipulationen "unbemerkt", was nicht den Anforderungen der digitalen Signatur entspricht.
Wird muss ein signiertes Dokument geändert werden, dann muss es erneut signiert werden, weil die alte Signatur nicht mehr zum Dokument passt.
Funktionsweise der digitalen Signatur
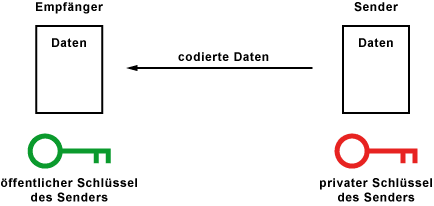
Die digitale Signatur basiert auf der asymmetrischen Kryptografie, wobei das verwendete asymmetrische Verfahren umgekehrt wird. Bei der asymmetrischen Verschlüsselung dient der öffentliche Schlüssel zum Verschlüsseln und der private Schlüssel zum Entschlüsseln. Bei der digitalen Signatur werden die Daten mit Kennzeichen versehen, die durch den privaten Schlüssel hinzugefügt werden. Mit dem öffentlichen Schlüssel kann man feststellen, ob die Daten von demjenigen stammen, der mit seinem privaten Schlüssel signiert hat und ob die Daten unverändert sind.
Die Tatsache, dass der private Schlüssel durch seinen Besitzer geheim gehalten wird, erlaubt die Annahme, dass Daten, die mit dem privaten Schlüssel codiert sind, tatsächlich vom Schlüsselbesitzer stammen.
Um Nachrichten und Dokumente zu signieren muss dessen Ersteller die Nachricht mit seinem privaten Schlüssel "entschlüsseln". Der dabei entstandene "Klartext" ist die digitale Signatur. Sie wird an das Dokument angehängt. Die Signatur kann von jedem anderen mit dem öffentlichen Schlüssel des Erstellers "verschlüsselt" werden. Dabei entsteht die ursprüngliche Nachricht, die mit der unverschlüsselten Nachricht verglichen werden kann. Sind beide gleich, ist das Dokument unverändert und korrekt signiert.
Blockweise erstellte Signaturen haben zusammen mindestens die gleiche Länge, wie die Nachricht oder das Dokument selbst. Das ist recht unpraktisch. Das Signieren kann ein erheblicher Aufwand bezüglich Aufwand und Rechenleistung sein. Ebenso die Prüfung der Signatur. Deshalb wird nie die ganze Nachricht signiert. Statt dessen wird aus der Nachricht zuerst eine Prüfsumme gebildet, die viel kürzer sein kann als die Nachricht selbst. Und erst dann wird das Signaturverfahren auf diese Prüfsumme angewendet.
Das Verfahren, mit dem die Prüfsumme gebildet wird, ist eine kryptografische Hash-Funktion. Das Ergebnis der kryptografischen Hash-Funktion ist der Hash-Wert oder auch nur Hash genannt.
Hinweis: Die digitale Signatur wird mit dem privaten Schlüssel erzeugt, womit die Echtheit beglaubigt und die Identität des Absenders bestätigt wird. Die Überprüfung der Echtheit der Nachricht und die Identität des Absenders erfolgt mit dem öffentlichen Schlüssel.
Wenn dem Besitzer des privaten Schlüssels dieser Schlüssel geklaut wird, dann kann eine andere Person im Namen des Besitzers Nachrichten und Dokumente signieren.
Signaturverfahren
Bekanntlich basieren Signaturverfahren auf asymmetrischen Verfahren, die sehr langsam arbeiten und von denen es nicht viele gibt. Das bekannteste und wohl am meisten eingesetzte Signaturverfahren ist RSA. Es gibt aber auch noch die Discrete Logarithm Signature Systems (DLSS). Dabei handelt es sich um eine Gruppe von Signaturverfahren auf Basis des diskreten Logarithmus. Dazu gehören ElGamal und DSA.
- RSA
- ElGamal
- DSA
Es gibt weitere DLSS-Verfahren, die in der Praxis nicht so häufig anzutreffen sind und deshalb hier nicht genannt werden.
RSA als Signaturverfahren
RSA ist eigentlich ein asymmetrisches Verfahren, das in der Hauptsache zum Verschlüsseln und Schlüsselaustausch eingesetzt wird. Weil Signaturverfahren mit Public-Key-Verfahren zusammenhängen, kann man RSA auch als Signaturverfahren einsetzen.
Mit RSA wird die digitale Signatur wie folgt umgesetzt:
- Ein Teilnehmer "unterschreibt" eine Nachricht m, indem er sie mit seinem privaten Schlüssel d kodiert. Heraus kommt die Signatur s.
- Er verschickt die Nachricht m zusammen mit der Signatur s.
- Die Echtheit der Nachricht m und die Identität der Person kann durch die Signatur s und den öffentlichen Schlüssel von jedem überprüft werden.
DLSS - Discrete Logarithm Signature Systems
Discrete Logarithm Signature Systems, kurz DLSS, sind Signaturverfahren auf Basis des Diffie-Hellman-Verfahrens.
DLSS haben gegenüber RSA verschiedene Nachteile. Zum einen sind sie beim Prüfen der digitalen Signatur etwa zehnmal langsamer. Das wiegt schon allein deshalb schwer, weil asymmetrische Verfahren generell langsam sind. Zweitens bedarf es beim Erstellen der Signatur einer Zufallszahl aus einem guten Zufallszahlengenerator, was nicht selbstverständlich ist.
DLSS-Verfahren können auch mit Hilfe elliptischer Kurven implementiert werden. Dadurch werden sie schneller als RSA. Auch RSA kann man mit elliptischer Kurven implementieren, was aber in der Praxis kaum eingesetzt wird.
ElGamal
Das einfachste DLSS ist das ElGamal-Verfahren von Taher ElGamal. Allerdings wird es so in der Praxis selten eingesetzt. Aber es bildet die Basis für das DSA-Verfahren.
Wie alle anderen DLSS-Verfahren ist ElGamal eine Weiterentwicklung des Diffie-Hellman-Schlüsselaustauschs.
DSA - Digital Signature Algorithm
DSA gehört zur Familie der DLSS-Verfahren, stammt aus der Feder der NSA (US-Geheimdienst) und ist Teil des DSS (Digital Signature Standard). DSS wurde von der US-amerikanischen Standardisierungsbehörde NIST 1991 veröffentlicht und 1994 standardisiert. Schon damals war RSA weit verbreitet. Allerdings stand RSA bis 2000 in den USA unter Patentschutz, weshalb sich die NIST für ein DLSS-Verfahren für den DSA entschieden hat. Allerdings findet DSA nur zum Erstellen und Verifizieren von Signaturen Anwendung.
Trotz des Patentschutzes für RSA ist das Misstrauen gegenüber einem Verfahren, in dem die NSA ihre Finger im Spiel hat, sehr groß. Durchaus begründet. Denn DSA hat eine bekannte Schwäche. Verwendet man bei der Verschlüsselung zwei mal den gleichen Zufallswert, dann kann der geheime Schlüssel aus einer einfachen arithmetischen Berechnung gebildet werden. DSA ist also anfällig für schlechte Zufallszahlengeneratoren oder schlechte Implementierungen. Da DSA das unsichere SHA-1 als kryptografische Hash-Funktion verwendet, gilt damit auch DSA als unsicher. Obwohl DSA ein internationaler Standard ist, ist es für die digitale Signatur eher zweite Wahl.
Wie sicher ist digitale Signatur mit RSA und DLSS?
Das Ziel eines Angriffs bei der digitalen Signatur ist es, den privaten Schlüssel (Private Key) des Nutzers herauszubekommen. Schafft es der Nutzer diesen Schlüssel vor fremder Einsichtnahmen und Diebstahl zu schützen, dann gibt es nur noch zwei Angriffsmöglichkeiten bei RSA. Einmal die vollständige Schlüsselsuche und ein Faktorisierungsangriff. Beides dürfte bei einer Schlüssellänge von 1.024 Bit ein schwieriges Unterfangen sein. Die Empfehlungen gehen jedoch zu einer Schlüssellänge von mindestens 2.048 Bit. In besonders kritischen Umgebungen kann man auch 4.096 Bit nehmen. Das ist insbesondere dann sinnvoll, wenn man das Schlüsselpaar nicht gleich tauschen will, wenn 2.048 Bit irgendwann als zu kurz angesehen wird.
Die gleiche Sicherheit erreicht man bei DLSS-Verfahren auch mit unwesentlich kürzeren Schlüsseln. Bei DLSS ist aber die Zufallszahl beim Signieren der Knackpunkt. Nicht alle Systeme können guten Zufall liefern. Das bedeutet, ein Angreifer könnte den Zufall erraten und so auf den Schlüssel schließen. Noch schlimmer wird es, wenn man zweimal den gleichen Zufall verwendet. Dann fällt auf der anderen Seite der geheime Schlüssel aus einer vergleichsweise einfachen arithmetischen Umformung heraus. Bei RSA ist die Signierung nicht von einem zusätzlichen Zufallswert abhängig. Bei RSA muss nur der Schlüssel einmal zufällig generiert werden, was auch weniger zeitkritisch ist.
Die größte Bedrohung geht aber nicht von einem Angreifer aus, der sich für den privaten Schlüssel interessiert. Viel gefährlicher ist der Angreifer, der die Signatur-Software kontrolliert. Der Angreifer könnte dann dafür sorgen, dass der Benutzer nicht das sieht, was er tatsächlich signiert. Das ist besonders dann gefährlich, wenn zum Signieren und Verschlüsseln der gleiche Schlüssel verwendet wird. Da bei RSA das Signierverfahren dem Entschlüsselungsverfahren entspricht entsteht hier der Klartext ohne das es der Nutzer merkt. Deshalb setzen die üblichen Implementierungen, die signieren und verschlüsseln jeweils unterschiedliche Schlüsselpaare ein. Unabhängig davon muss der Anwender beim Einsatz von Signatur-Software sicherstellen, dass er einen sauberen und sicheren PC verwendet.
Ob man RSA oder DLSS, wie DSA, einsetzt ist eher Geschmackssache. RSA gilt schon als ziemlich alt. Deshalb wird oft ECDSA, also elliptische Kurven (ECC) in Kombination mit DSA empfohlen. Doch radikale Kryptografen lassen kein gutes Haar an den von der NSA beeinflussten elliptischen Kurven und DSA. Beide sind sehr anfällig für schlechte Zufallszahlengeneratoren. So gesehen hat das bewährte RSA mit 4.096 Bit Schlüssellänge noch lange nicht ausgedient.