Rauschdämpfung mit Tiefpassfilter
Inhaltsverzeichnis
- Lerninhalte
- Rauschen, immer und überall
- Nicht alles was klein ist, ist auch fein...
- Wichtiger Hinweis!
- Der LinCMOS-Operationsverstärker
- Rauschspannungsdichte und Rauschspanung
- Rauschverminderung durch Begrenzung des Frequenzbandes
- Ungeeignete Lösung mit der Unitygain-Bandbreite
- Zuviel Rauschen oder Übersteuerung
- Die präzise Lösung
- Filter gleich im Verstärker implementiert
Lerninhalte
Wir lernen in kurzen Zügen etwas über die Ursachen des Rauschens und wir werfen auch einen Blick hinaus in den Kosmos und betrachten den Rauschhintergrund. Danach thematisieren wir kurz die Störsignale generell - Rauschen gehört dazu - welche dann signifikant in Erscheinung treten, wenn man es mit kleinen Signalen zu tun hat. Parallel zur Rauschdämpfung durch Reduktion der Frequenzbandbreite mittels Tiefpassfilterung, lernen wir die LinCMOS-Opamp-Familie von Texas Instruments kennen. Wir wollen wissen was der Unterschied zwischen Rauschspannungsdichte und Rauschspannung ist. Weiterer Lernnebeneffekt: Warum macht es Sinn hohe Verstärkungen auf zwei Opamps (Operationsverstärker) zu verteilen? Praxis: Rauschdämpfung mit Tiefpassfilter mit guter Frequenzlinearität und ein stark vereinfachtes Prinzip mittels Verstärker und Filter in einem, wenn es die Anwendung zulässt. Die optimale Arbeitspunktspannung ist ebenfalls ein Thema dieses Elektronik-Minikurses.
Rauschen, immer und überall
Ich erwähne jetzt zwei unterschiedliche Ursachen wie Rauschspannungen
entstehen. Die eine kommt infolge der Wärmebewegungen von elektrischen
Ladungsträgern zustande und die andere durch Halbleiterübergänge, wenn
eine so hohe Spannung anliegt, dass Durchbrucheffekte entstehen. Im
Falle einer Strombegrenzung, welche die Zerstörung des Bauteils
vermeidet, erzeugen die "durchbrechenden" Ladungsträger Stromimpulse,
die sich im Mittelwert als Rauschstrom, bzw. Rauschspannung, bemerkbar
machen.
Mit dieser Methode kann man einfach und preiswert Rauschgeneratoren
realisieren: Man verwendet den Basis-Emitter-Übergang eines NPN- oder
PNP-Transistors im inversen Betrieb. Der Basis-Emitter-Übergang verhält
sich dabei wie eine Zener-Diode mit einer Durchbruchspannung von etwa 6
V. Bei einem gewissen kleinen Emitter-Basis-Strom, erreicht man
einigermassen eine Gaussverteilung der Rauschspannung im Bereich einiger
Millivolt bis wenigen zehn Milivolt. Die Exemplarstreuung zwischen
verschiedenen Transistortypen ist ziemlich gross. Mit nachträglich
ausreichender Verstärkung hat man einen preiswerten breitbandigen
Rauschgenerator mit weissem Rauschen.
Es gibt nichts das nicht rauscht. Jedes Objekt das nicht absolut kalt
ist, d.h. eine Temperatur von mehr als 0 K (-273.16°C) hat, dessen
Elektronen und andere Ladungsträger bewegen sich und das Objekt rauscht.
Wie hoch die Rauschspannung eines Widerstandes ist, ist abhängig von
seiner aboluten Temperatur, von der Grösse des Widerstandes, von einer
Naturkonstante - die sogenannte Bolzmann-Konstante mit einem Wert von
1.38*10-23*Ws/K - und von der Frequenzbandbreite der
Rauschspannung. Dieses Rauschen begleitet die Physik und damit die
Elektrotechnik auf allen Wegen, ganz besonnders wenn man es mit kleinen
Signalen zu tun hat.
Für alle die es interessiert, werfen wir jetzt kurz einen Blick in den
Kosmos...
Wenn es so ist, dass jedes Ding rauscht, das wärmer ist als 0 K, muss
auch der Kosmos rauschen, wenn dieser nicht absolut kalt ist. Tatsache
ist, dass der Kosmos als Ganzes ein schwaches Hintergrundrauschsignal,
mit beinahe homogen verteilter Intensität, sendet, das einer absoluten
Temperatur von 2.73 K entspricht. Die Entdecker dieses Rauschens waren
die beiden Astrophysiker Arno Penzias und Robert Wilson. Ihre Entdeckung
gelang ihnen mit einer 6-Meter-Hornreflektorantenne im Jahre 1964. Man
interpretiert diese homogene Hintergrundstrahlung - das Echo einer
glühenden kosmischen Vergangenheit - als ein schwaches Nachleuchten aus
der ultraheissen Epoche des "Urknalls". Dies war vor etwa 14 Milliarden
Jahren. Es sei an dieser Stelle noch angemerkt, dass sich heute die
Kosmologen gar nicht mehr so einig darüber sind, ob es den "Urknall"
überhaupt gab. Es gibt mittlereweile alternative Modelle, die aber nicht
Teil dieses Elektronik-Minikurses sein können...
Das farbige Bild oben illustriert in Falschfarbendarstellung die
äusserst schwachen Unregelmässigkeiten (Fluktuationen) der kosmischen
Hintergrundstrahlung, mit einer Abweichung von 1/100'000 im Vergleich zu
den 2.73 K - aufgenommen vom Satelliten COBE. Das Bild stammt vom
Institute of Astronomy ETH Zurich.
Nicht alles was klein ist, ist auch fein...
Wenn man sehr kleine Spannungen misst, ist man mit Störspannungen konfrontiert. Dies sind Einwirkungen von elektrischen, magnetischen und elektromagnetischen Feldern. Es gibt thermisch bedingte Störspannungen (Lötstellen, Kontakte, Halbleiterübergänge), es gibt systeminhärente (z.B. Opamps) und externe (z.B. Sensoren) Rauschspannungen und es gibt auch störende mechanische Einflüsse, wie z.B. Piezzo- oder Ladeveschiebungseffekte. Dazu kann man ein einfaches Experiment anstellen: Man schliesse ein offenes abgeschirmtes Kabel mit sehr kurzen Drahtenden an einen Oszilloskopen, der auf maximale Empindlichkeit eingestellt wird. Nun spicke man mit dem Finger ans isolierte Kabel und man sieht einen schönen Spannungsimpuls in Form einer aperiodischen Schwingung auf dem Bildschirm. Das selbe kann man beobachten, wenn man an einen Keramikkondensator spickt oder an ihm kratzt, wenn dieser in einem hochempfindlichen Pfad einer Verstärkerschaltung eingebaut ist. Daher muss man gut darauf achten, wo man Keramik-Kondensatoren einbaut, auf dass nicht die gesamte Verstärkerschaltung gleich zum ungewollten Mikrofon oder Vibrationsmessgerät wird. Nun, was uns hier wirklich interessiert, ist die Rauschspannung und eine Art des praktischen Umgangs mit ihr.
Wichtiger Hinweis!
In diesem Elektronik-Minikurs dient die Elektronik der Elektromyographie (EMG) als Beispiel, da sie sich gut dafür eignet ein praktisches Beispiel der Rauschverminderung durch Reduktion der Frequenzbandbreite des Verstärkers zu erklären. Ich weiss von vielen E-Mails, dass EMG unter den Lesern meiner Elektronik-Minikurse auf grosse Resonanz stösst. E-Mails, die das EMG-Interesse kundtun, Fragen oder Ideen enthalten, beantworte ich gerne, wenn es zeitlich möglich ist. Da dies jedoch ein Elektronik-Minikurs ist, haben E-Mails mit Fragen oder Ideen zum elektronischen Inhalt Priorität. Ich hoffe, ich stosse dabei auf Verständnis.
Der LinCMOS-Operationsverstärker
Die hier verwendeten Opamps sind sogenannte LinCMOS-Typen von
Texas-Instruments.
Sie eignen sich für Single-Supply-Anwendungen (z.B. +5 VDC). Dies
bedeutet, die Spannung an ihren Eingängen darf den Wert von GND haben,
ohne dass die Opamps in ihrer Funktionalität wesentlich eingeschränkt
werden. Die Ausgangsspannung geht ebenfalls bis auf GND hinunter, sofern
der Ausgang nicht mit einem signifikanten Strom im mA-Bereich belastet
wird. Die Eingangsspannung darf maximal 1 VDC unterhalb der
Betriebsspannung liegen und die maximal mögliche Ausgangsspannung liegt
ebenfalls etwa 1 VDC unterhalb der Betriebsspannung, auch wenn die
Strombelastung noch so gering ist. LinCMOS-Opamps sind daher keine
Rail-to-Rail-Opamps.
Die LinCMOS-Opamps gibt es in der Single-, Dual- und Quadversion. Bei
der Dual- und Quad-Version gibt es Typen für den Low-, Medium- und
High-Bias-Mode. Bei der Single-Version gibt es nur gerade einen Typ. Er
hat jedoch einen Steuereingang um den Opamp in den Low-, Medium- oder
High-Bias-Mode zu schalten. Der Low-Bias-Mode benötigt am wenigsten
Betriebsstrom (Betriebsleistung), dafür arbeitet er am langsamsten, d.h.
dieser Mode hat die geringste Unity-Gain-Bandbreite und den niedrigsten
Slewrate. Er eignet sich besonders für Batterieanwendungen. Genau
umgekehrt verhält sich der High-Bias-Mode. Er ist schnell und benötigt
dafür am meisten Power. Der Medium-Bias-Mode liegt in dier Mitte, - ein
oft guter Kompromiss.
Will man sich, wie eben angedeutet, auf den Single-Opamp beschränken, hat
man die Möglichkeit den Bias-Mode, bzw. Strom-/Leistungsverbrauch, in
den selben drei Stufen mit einem Opamp zu wählen. Dafür benutzt man den
Opamp TLC271 mit seinem Anschluss Bias-Select (Pin 8). Liegt er auf
positiver Betriebsspannung, ist dies der Low-Bias-Mode. Auf halber
Betriebsspannung gilt der Medium-Bias- und auf GND-Pegel der
High-Bias-Mode. Wenn der Opamp mit Dual-Supply (z.B. ± 2.5 VDC)
betrieben wird, muss für Medium-Bias (mittleren
Strom-/Leistungsverbrauch und mittlere Geschwindigkeit) der
Bias-Select-Anschluss mit GND verbunden werden.
Texas-Instruments bietet
Datenblätter zu diesen LinCMOS-Opamps, die gut dokumentiert sind. Das
Datenblatt zum
TLC271
enthält alleine 31 Funktionsdiagramme für den High-Bias-Mode. Es lohnt
sich dies anzusehen!
Noch etwas anderes ist sehr wichtig zu wissen: Je geringer der
Leistungsverbrauch eines Opamps einer beliebigen Opampfamilie ist, desto
höher ist seine Rauschspannungsdichte. Dies gilt generell. Beim
LinCMOS-Typ TLC271 beträgt die äquivalente
Eingangs-Rauschspannungsdichte in der High-Bias-Betriebsart
25 nV/Hz0.5, in der Medium-Bias-Betriebsart
32 nV/Hz0.5 und in der Low-Bias-Betriebsart
68 nV/Hz0.5. Für die Dual- und Quad-Version gelten TLC272 bzw.
TLC274 als High-Bias-Mode, TLC27M2 bzw. TLC27M4 als Medium-Bias-Mode und
TLC27L2 bzw. TLC27L4 als Low-Bias-Mode.
Die Tatsache, dass die äquivalente Eingangs-Rauschspannungsdichte
generell umgekehrt proportional zum Leistungsverbrauch und der
Geschwindigkeit (Unity-Gain-Bandbreite und Slewrate) ist, sieht man sehr
gut bei Vergleichen von andern Opamps. Hier ein Vergleich der beiden
Bi-FET-Opamp-Familien TL071 (Single), TL072 (Dual), TL074 (Quad) mit
TL061 (Single), TL062 (Dual), TL064 (Quad). Die TL07x-Familie benötigt
einen Strom von 2.5 mA pro Opamp, hat eine Unity-Gain-Bandbreite von 3
MHz und einen Slewrate von 13 V/µs mit einer Rauschdichte von 18
nV/Hz0.5. Die Lowpower-TL06x-Familie, welche sich besonders
für den Batteriebetrieb eignet, benötigt einen Strom von nur 0.25 mA pro
Opamp, hat eine Unity-Gain-Bandbreite von 1 MHz, einen Slewrate von 3.5
V/µs mit einer Rauschspannungsdichte von 35 nV/Hz0.5. Ein
anderes Beispiel von National-Semiconductor (ursprünglich):
Der Single-Opamp LF351 benötigt einen Strom von 1.8 mA, hat eine
Unity-Gain-Bandbreite von 4 MHz, einen Slewrate von 13 V/µs mit einer
Rauschspannungsdichte von 25 nV/Hz0.5. Sein Lowpower-Pentant,
der Single-Opamp LF441 benötigt einen Strom von bloss 0.15 mA, hat eine
Unity-Gain-Bandbreite von 1 MHz, einen Slewrate von 1 V/µs mit einer
Rauschspannungsdichte von 35 nV/Hz0.5.
Irgendwann in den 1980er-Jahren unternahm
Texas-Instruments
eine Anstrengung die auseinanderklaffenden Daten, wie je geringer der
Leistungsverbrauch desto höher die Rauschspannungsdichte, zu veringern.
Dies gelang ihr mit dem Entwurf der Excalibur-Opamp-TLE-Familien, die es
in Normalpower-, Lowpower-, Single-, Dual- und Quad-Ausführung gibt.
Rauschspannungsdichte und Rauschspannung
Anfängern bietet das Datenblatt eines praktisch jeden Opamps einiges
Kopfzerbrechen. Da liest man in der Tabelle unter dem Parameter
'Equivalent Input Noise Voltage' bei den Einheiten nicht etwa
'nV', sondern 'nV/Hz0.5'. Ausgeprochen heisst
dies Nanovolt pro Quadratwurzel aus einem Hz. Das ist aber
die Rauschspannungsdichte und nicht die Rauschspannung. Dass die
Rauschspannungsdichte angegeben wird, macht aber viel Sinn, wie wir noch
sehen werden.
Zunächst noch folgendes: Da es mir nicht möglich ist im Text ein
Wurzelzeichen anständig hinzukriegen, wähle ich die exponentielle
Darstellung, was in diesem Zusammenhang zwar ungewohnt ist, aber ebenso
gut geht. Die Qudtratwurzel aus x, ist identisch mit x0.5,
wie es links im Kästchen im folgenden Bild 1 gezeigt wird:
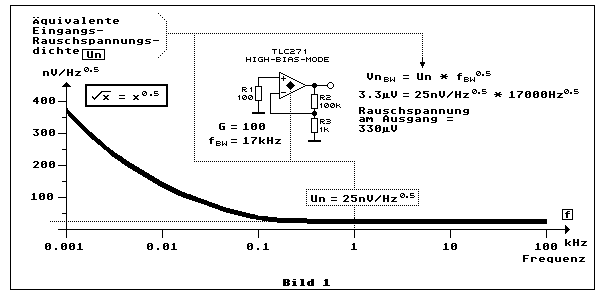
Bild 1 zeigt die typische Kurve der Rauschspannungsdichte eines Opamp,
allerdings mit jeweils unterschiedlichen Werten. Das Typische ist, dass
die Rauschspannungsdichte oberhalb einer gewissen Frequenz konstant,
unterhalb dieser jedoch erheblich zunimmt. Die Opamp-Hersteller bemühen
sich für hochwertige Opamps diese Eckfrequenz so niedrig wie möglich zu
realisieren. Die Rauschspannungsdichte wird oft bei einer Frequenz von 1
kHz angegeben, was nichts anderes heisst, als dass die
Rauschspannungsdichte bei dieser Frequenz und darüber etwa im konstanten
Bereich liegt.
Worin liegt aber der Sinn, dass die Rauschspannungsdichte und nicht die
Rauschspannung angegeben wird? Diese Frage ist eigentlich nicht ganz
richtig, weil oft zusätzlich die Rauschspannung angegeben wird. Diese
Rauschspannung wird und muss aber stets innerhalb einer Frequenzbandbreite
definiert angegeben werden, weil die Rauschspannung davon direkt
abhängig ist. So liest man im Datenblatt des
LF400,
einem speziellen Opamp von National-Semiconductor, neben einer
Rauschspannungsdichte von 23 nV/Hz0.5, die Rauschspannung von
2.3 µVrms bei einer Frequenzbandbreite zwischen 10
Hz und 10 kHz.
Kommen wir zur Frage zurück, warum Rauschspannungsdichte? Diese Angabe
macht es dem Anwender besonders leicht, die effektive Rauschspannung für
eine beliebige Frequenzbandbreite, die im Bereich der einigermassen
konstanten Rauschspannungsdichte liegt, zu berechnen. In Bild 1
illustriert dies ein einfaches Beispiel mit dem LinCMOS-Opamp TLC271 in
der High-Bias-Betriebsart. Die Unity-Gain-Bandbreite liegt bei 1.7 MHz.
R2 und R1 ergeben eine Verstärkung von 100. Damit hat dieser Verstärker
eine Frequenzbandbreite von 17 kHz, - eine Bandbreite die für die
meisten Audioanwendungen genügt. Nun stellt sich die Frage, wie gross
bei dieser Bandbreite die äquivalente Eingangsrauschspannung ist. Wie
sie berechnet wird, zeigt ebenfalls Bild 1. Sie beträgt
3.3 µVrms oder die Ausgangsrauschspannung beträgt
330 µVrms.
Neben der Bezugsfrequenz - hier und sehr oft 1 kHz - ist ein weiterer
wichtiger Parameter für die Rauschspannungsdichte der maximale Wert des
angeschlossenen Widerstandes R1. Oft ist dieser mit 100 Ohm oder bei
Very-Low-Noise-Opamps mit weniger oder sogar 0 Ohm angegeben. Dieser
Widerstand muss so niederohmig sein, dass seine Rauschspannung
wesentlich unter der äquivalenten Rauschspannung des Opamp bleibt.
Fragt sich bloss, was bedeutet eigentlich das Wort äquivalent?
Die Eingangsverstärkerstufe des Opamp verursacht selbst ein
Spannungsrauschen und dies ist vergleichbar mit einem idealen Opamp der
gar nicht rauscht und einem externen Widerstand der eine Rauschspannung
liefert. Ganz wichtig: Mit diesem "gedachten" Widerstand ist nicht R1 in
Bild 1 gemeint.
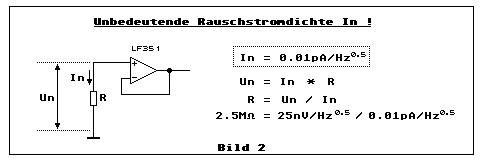
Jeder Opamp hat zur Rauschspannungsdichte auch noch eine
Rauschstromdichte. Der daraus resultierende Rauschstrom, der ebenso von
der Frequenzbandbreite abhängig ist, erzeugt über einem angeschlossenen
Widerstand R - der den Innenwiderstand der Spule eines dynamischen
Mikrophones sein kann - eine Rauschspannung. Diese addiert sich
quadratisch zur Rauschspannung des Opamp. Da wir uns hier mit CMOS- und
auch etwas mit BiFET-Opamps befassen, gehe ich nicht ins Detail. Es ist
schlichtweg nicht nötig. Bild 2 illustriert, dass die Rauschstromdichte
so niedrig ist, dass beim LF351 (BiFET-Opamp) oder aber auch beim LMC271
(LinCMOS: High-Bias-Mode) der Widerstand R einen hohen Wert von 2.5
M-Ohm haben muss, dass die erzeugte Rauschspannungsdichte gleich gross
ist wie die Rauschspannungsdichte des Opamp. In der Praxis bedeutet
dies, dass bei R1 = 1 M-Ohm, dessen Rauschspannung, der durch den
Rauschstrom des Opamps verursacht wird, unbeachtet bleiben kann. Aber
Vorsicht: Ein so hoher Widerstand rauscht von selbst, ohne dass ein
Rauschstrom durch ihn hindurchfliesst. Bei Raumtemperatur erzeugt ein
Widerstand mit 1 M-Ohm eine Rauschspannungsdichte von etwa 160
nV/Hz0.5 und das ist viel mehr als die Rauschspannungsdichte
des Opamps. Gerade auch aus diesem Grund kann man sagen, dass sich ein
Opamp mit einer FET- oder MOSFET-Eingangsstufe, bezüglich Stromrauschen,
praktisch ideal verhält, weil die Realität wird durch die äquivalente
Rauschspannung des Opamp und/oder durch das Widerstandsrauschen von R
bestimmt.
Zu diesem Thema und allen andern Themen die mit Kleinsignalen zu tun
haben, empfehle ich das Buch "Die Verarbeitung von Kleinsignalen in
elektronischen Systemen" von Roland Best vom AT-Verlag (ISBN:
3-85502-114-7). Roland Best's Bücher zu verschiedenen Themen der
Elektronik sind generell sehr empfehlenswert!
Rauschverminderung durch Begrenzung des Frequenzbandes
Im vorherigen Kapitel haben wir gelernt, dass die Rauschspannung umso
grösser ist, je grösser die Bandbreite der Frequenz ist. Diesmal geht's
in die umgekehrte Richtung: Wir haben eine Signalquelle mit einer
Rauschspannung. Da diese zu hoch ist, dämpfen wir sie durch Reduktion
der Frequenzbandbreite. Dies ist dann zulässig, wenn die reduzierte
Bandbreite, die Bandbreite des Signals nicht oder nur unwesentlich
beeinträchtigt. Würde man in einer solchen Situation keine
Bandbegrenzung vornehmen, verschenkt man sich eine niedrigere
Rauschspannung und somit ein besseres Signal/Rausch-Verhältnis
(Signal/Noise-Ratio). Dieser Wert gibt an, wie hoch das Verhältnis aus
maximal möglicher oder maximal zulässiger Signalsspannung zur
Rauschspannung ist. Diese Angabe erfolgt in der Regel in Dezibel (dB).
Dazu die Berechnungsformel:
S/N-Ratio(dB) = 20 * log
(USignal /
UNoise)
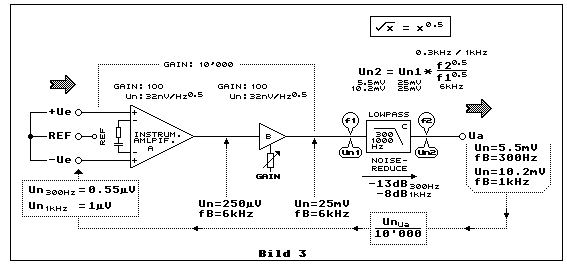
Das Blockschaltbild in Bild 3 illustriert ein praktisches Beispiel. Der
Instrumentationsverstärker
verstärkt mittels Elektroden an +Ue und -Ue ein bioelektrisches Signal.
Es ist hier ein elektromyographisches Signal (EMG-Signal), das mittels
Hautoberflächenelektroden gemessen werden soll. Einfachheitshalber
betrachten wir jetzt allerdings die kurzgeschlossenen Eingänge, weil uns
nur interessieren soll, was mit der äquivalenten Rauschspannung des
Instrumentationsverstärkers geschieht.
Die Rauschspannungsdichte liegt bei 32 nV/Hz0.5. Die
Frequenz-Bandbreite liegt bei 6 kHz, die sich aus der
Unity-Gain-Bandbreite und der Verstärkung ergibt. Aus dieser Bandbreite
und der Rauschspannungsdichte errechnet sich die Rauschspannung zu 250
µV, die mit IC:B zu maximal 25 mV verstärkt wird. Dividieren wir jetzt
diese Rauschspannung durch die maximale Gesamtverstärkung von IC:A
(Instrumentation-Amplifier) und IC:B (Opamp), ergibt dies eine
äquivalente Eingangsrauschspannung von 2.5 µV, und dies bezogen auf
eine Frequenzbandbreite von 6 kHz!
Da schwache EMG-Signale sehr klein sein können und eine wesentlich
geringere Bandbreite haben, reduzieren wir die Rauschspannung, in dem
wir ein Tiefpassfilter (LOWPASS) nachschalten. Die Rauschspannung vor
dem Tiefpassfilter ist mit Un1 und diejenige nach dem Tiefpassfilter mit
Un2 bezeichnet. Oberhalb dieses Tiefpassfilterblocks sieht man die
Formel, welche zeigt, wie Un2 aus Un1 und dem Verhältnis von f2 (nach dem
Tiefpassfilter) zu f1 (vor dem Tiefpassfilter) berechnet wird. Un2
wird für zwei Grenzfrequenzen berechnet, für 300 Hz und 1 kHz. Für 300
Hz beträgt die Ausgangsrauschspannung 5.5 mV, was einer äquivalenten
Eingangsrauschspannung von 0.55 µV entspricht. Dies bedeutet eine
Dämpfung der Rauschspannung von immerhin 13 dB, wobei 12 dB einem
Faktor 4 entspricht. Wählt man eine Grenzfrequenz von 1 kHz, ist die
Ausgangsrauschspannung mit 10.2 mV fast doppelt so hoch. Sie entspricht
einer äquivalenten Eingangsrauschspannung von 1 µV. Die Dämpfung der
Rauschspannung beträgt noch 8 dB, was fast einem Faktor 3 entspricht.
Mit einer Bandbegrenzung von 300 Hz oder auch 1 kHz - es kommt etwas auf
die Anwendung an - liegt man für Oberflächen-EMG-Messungen, wie bereits
angedeutet, richtig. Für EMG-Biofeedback-Anwendungen genügen 300 Hz. Wir
betrachten jetzt kurz den Rauschzustand, wenn die Eingänge +Ue und -Ue
mit REF (Neutral-Elektrode) nicht kurzgeschlossen, sondern mit
Elektroden und Leitpasta an einem Muskel sauber fixiert sind. Jetzt
müssen wir einkalkulieren, dass wir es beim Haut-Elektroden-Kontakt u.a.
mit einem ohmschen Widerstand im 10-k-Ohm- bis 100-k-Ohm-Bereich zu tun
haben und diese "Widerstände" erzeugen auch ein biologisch bedingtes
Rausch-, bzw. Störsignal. Dies wird hier nicht weiter thematisiert, weil
es sonst den Rahmen schnell sprengen würde. Ich will hier bloss
andeuten, dass nur schon der Quellwiderstand auch eine rein
widerstandsabhängige Rauschspannung liefert, welche jedoch durch die
Tiefpassfilterung ebenfalls gedämpft wird. Mehr zum
widerstandsabhängigen Rauschen liest man im weiter oben empfohlenen Buch
von Roland Best im Kapitel Rauschen. In den folgenden Kapiteln
befassen wir uns mit den Möglichkeiten das Rauschen mittels
Tiefpassfilter zu reduzieren.
Ungeeignete Lösung mit der Unitygain-Bandbreite
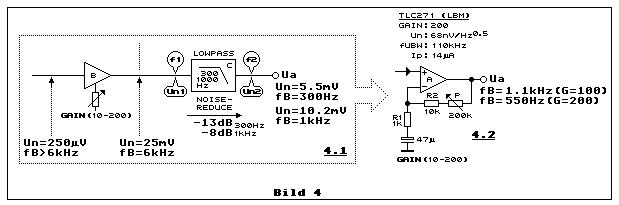
Wir stellen uns hier zunächst die Frage, wie einfach man eine
Rauschreduktion mittels Bandbegrenzung realisieren kann, denn der Opamp
selbst, bietet bei genügend hoher Verstärkung eine genügend niedrige
Frequenzbandbreite, um damit die Rauschspannung zu dämpfen. Teilbild 4.2
zeigt eine Möglichkeit, wie der Filterteil in Teilbild 4.1 (Ausschnitt
aus Bild 3), mit dieser Methode umgesetzt werden kann. Im Prinzip
schlägt man mit dieser Schaltung zwei Fliegen auf einen Schlag: Man hat
einen Verstärker und ein Tiefpassfilter. Ob dieser Schlag allerdings so
toll ist oder eher ins Wasser geht, wird sich gleich zeigen...
IC:A ist ein LinCMOS-Opamp des Types TLC271 im Low-Bias-Mode (Bild 4:
LBM). Dadurch ist er mit einem Betriebsstrom von bloss 14 µA sehr
sparsam und für den Batteriebetrieb geeignet. Die Unity-Gain-Bandbreite
beträgt dabei 110 kHz und die Rauschspannungsdichte
68 nV/Hz0.5. Man kann diese Methode durchaus anwenden, aber
man beachte, dass die Frequenzbandbreite stark davon abhängig ist, wie
gross die Verstärkung eingestellt ist. Dies bedeutet natürlich, dass die
Rauschspannung am Ausgang von der Verstärkung (Potmeter P) und der
dadurch veränderten Bandbreite abhängt. Um mit der Unitygain-Bandbreite
des Opamps als einfaches Tiefpassfilter zu arbeiten, setzt es voraus,
dass die Verstärkung fest eingestellt ist. Dazu kommt, dass man einen
Kompromiss zwischen Verstärkung und Filtergrenzfrequenz eingehen muss,
weil der Opamp mit der dazu idealen Unitygain-Bandbreite kaum gefunden
wird. Dazu kommt, dass die Unitygain-Bandbreite stark temperaturabhängig
ist. Von dieser Billigmethode ist also dringend abzuraten!
Zuviel Rauschen oder Übersteuerung
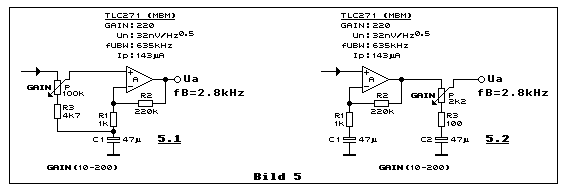
Wir bleiben mit Bild 5 noch ein wenig beim selben Thema. Beide
Verstärker in Bild 5 haben gemein, dass sie gleich hohe Verstärkungen,
hier einen Wert von 220, aufweisen. Es ist hier ebenfalls der
universelle LinCMOS-Opamp TLC271 im Einsatz. Diesmal allerdings im
Medium-Bias-Mode (MBM). Mit 32 nV/Hz0.5 ist die
Rauschspannungsdichte weniger als halb so gross wie im Low-Bias-Mode.
Die Unity-Gain-Bandbreite ist mit 635 kHz beinahe sechs mal grösser. Bei
einer Verstärkung von 220 beträgt die Bandbreite noch 2.8 kHz. Für eine
Bandbreite von 1 kHz, müsste die Verstärkung einen Wert von mehr als 600
haben und bei 300 Hz sogar 1800. Super, könnte man denken, weil mit der
indirekten Einstellung der Verstärkung mit P, in beiden Teilbildern,
beeinflusst man die Verstärkung der Opampschaltung nicht und man schlägt
zwei Fliegen auf einen Schlag: Hohe Verstärkung und man hat die
Frequenzbandbreite die man haben möchte.
Leider zu früh gefreut, weil eine solche Schaltung hätte andere ganz
massive Nachteile! Die Schaltung in Teilbild 5.1 erzeugt eine unnötig
hohe Rauschspannung auch dann wenn die Gesamtverstärkung mit P niedrig
eingestellt ist. Der Opamp in der Schaltung in Teilbild 5.2 wird
hoffnungslos übersteuert, wenn die Eingangsspannung, bezüglich der
Verstärkung, gegeben durch R2 und R1, zu hoch ist. Wegen diesen beiden
Nachteilen sind beide Schaltungen bereits unbrauchbar. Aber es gibt noch
einen dritten Nachteil, der beiden Schaltungen anhaftet, der allerdings
nur dann zutrifft, wenn die Schaltungen im Single-Supply-Mode (nur eine
positive Betriebsspannung) zum Einsatz kommt und mit C1 die
Arbeitspunktspannung entkoppelt werden muss, wie in Bild 5 gezeigt wird.
C1 braucht es in den beiden Schaltungen, um sicher zu stellen, dass sich
am invertierenden Eingang des Opamp die selbe Arbeitspunktspannung (oft,
aber nicht immer die halbe Betriebsspannung) einstellt, wie am
nichtinvertierenden Eingang. R1 und C1 haben somit die Wirkung eines
passiven Hochpassfilters erster Ordnung und bei angegeber
Dimensionierung beträgt die Grenzfrequenz 3 Hz. Das ist ein vernünftiger
Wert, wenn man es mit der Messung von niedrigen Frequenzen im
100-Hz-Bereich zu tun hat.
Man muss sich allerdings auch überlegen, was geschieht wenn die
Schaltungen in Teilbild 5.1 oder 5.2 eingeschaltet werden. C1 ist
zunächst entladen. R1 und R2 wirken als Spannungsteiler. Bei diesem
hohen R2/R1-Verhältnis liegt der invertierende Eingang zunächst fast auf
GND-Potential. Das heisst, der invertierende Eingang ist negativer als
der nichtinvertierende Eingang und somit liegt der Ausgang des Opamps
auf maximal positiver Spannung. Dies ermöglicht das Laden von C1 über R2
und R1. Aber das dauert relativ lange. Bei 220 k-Ohm und 47 µF beträgt
die Zeitkonstante 10 Sekunden. Bis die Verstärkerschaltung die korrekte
Arbeitspunktspannung erreicht hat, dauert es gut eine Minute. Um so
länger dauert diese Prozedur, wenn R2, auf Grund einer höheren
Verstärkung, noch grösser ist. Also, auch aus diesem Grund eignen sich
diese beiden Schaltungen nicht.
Die präzise Lösung
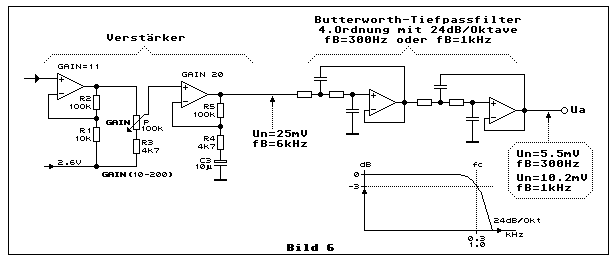
Bild 6 zeigt eine saubere und präzise Lösung, wo Verstärker und
Filter getrennt sind. Die Verstärkung von etwas mehr als 200 wird in
zwei Stufen aufgeteilt. Diese Gesamtverstärkung dürfte ohne weiteres
auch wesentlich höher sein. Die Einstellung der Gesamtverstärkung
zwischen den beiden Verstärkerstufen, ermöglicht das Ausgangsrauschen in
vernünftigen Grenzen und das Risiko der Übersteuerung durch zu hohe
Eingangsspannung gering zu halten. Man kann die Verstärkungsanteile
nach Bedarf auch umverteilen. Dies soll z.B. heissen: Wenn bei
vorliegender Dimensionierung eine Übersteuerung um mindestens 10 dB
nicht erreicht werden kann, kann man die Verstärkung des ersten
Verstärkers um 10 dB erhöhen und die Verstärkung des zweiten um den
selben Betrag verringern. Damit reduziert man das Rauschen des zweiten
Verstärkers.
Wie es zu der Arbeitspunktspannung von 2.6 VDC kommt, siehe folgendes
Kapitel Filter gleich im Verstärker implementiert.
Am Ausgang erfolgt beispielsweise ein aktives Butterworth-Tiefpassfilter
vierter Ordnung. Dies garantiert einen relativ linearen Frequenzgang bis
nahe an die Grenzfrequenz fc und danach folgt ein relativ steiler Abfall
der Amplitude von 24 dB/Oktave. Selbstverständlich kann man auch
steilflankigere Tiefpassfilterschaltungen einsetzen.
Wir befassen uns hier nicht im Detail mit aktiven Tiefpassfiltern. Man
kann sich mit diverser Elektronik-Litaratur schlau machen. Wie schon so
oft, empfehle ich auch hier das Buch Halbleiter-Schaltungstechnik von
U.Tietze und Ch. Schenk. Ein anderes sehr praxisbezogenes Buch ist das
Filter-Kochbuch oder Filter-Cookbook von Don Lancaster. Soweit mir
bekannt ist, gibt es nur noch die englischsprachige Originalausgabe. Der
Vorteil dieses Buches ist es, dass man mit wenig mathematischem Ballast
schnell zu brauchbaren Ergebnissen kommt. Wer im Besitze eines alten
ATARI-ST-Rechners ist, kann sich meine Programmsammlung als ZIP-Datei
herunterladen. Mehr dazu erfährt man in
ELEC2000, Praxisnahe Rechenprogramme für die Elektronik. Neben vielen andern Elektronik-Utilities, hat es ein
Programm zur Berechnung aktiver Hoch- und Tiefpassfilter für zweite,
vierte und sechste Ordnung. Das Programm heisst FILTCOOK. Grundlage
dieses Programmes ist das erwähnte Filterkochbuch von Don Lancaster.
Diese Elektronik-Utilities laufen auch unter einem ATARI-ST-Emulator.
Mit Garantie laufen diese Programme allerdings nur dann, wenn als
Betriebssystemversion ein Imagefile des TOS-1.04 verwendet wird.
Filter gleich im Verstärker implementiert
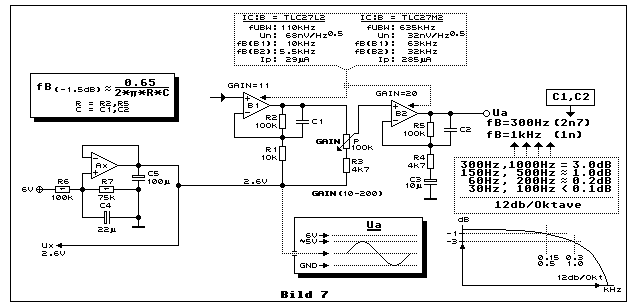
Die in Bild 7 gezeigte Schaltung ist der uns hier interessierende Ausschnitt einer grösseren Gesamtschaltung (EMG-Verstärker), die hier zu sehen ist. Man betrachte die Arbeitspunktspannung (Bezugsspannung) Ux, die in der Regel die halbe Betriebsspannung ist, jedoch auch einen davon abweichenden Wert haben kann. Ein Grund dafür wird in diesem Kapitel erklärt. Es geht dabei auch darum, wie man eine solche Arbeitpunktspannung erzeugt und was die Anforderungen dazu sind. Mehr im Detail dazu erfährt man im Kapitel "Die Ub/2-Referenz und der synthetische GND" im Elektronik-Minikurs:
- Operationsverstärker I (Zum weiteren Verständnis muss man nicht jetzt zu diesem Link wechseln!)
Opamp IC:Ax ist ein Opamp aus einem beliebigen Dual- oder Quad-Opamp. Es
darf natürlich auch ein Single-Opamp sein. Die Schaltung mit IC:Ax
erzeugt die Arbeitspunktspannung Ux, welche der
Verstärker/Filter-Schaltung und aller andern Teile der Gesamtschaltung
dient. Dies ist nötig, weil die gesamte Schaltung mit nur einer
Betriebsspannung (Single-Supply) gespiesen wird. Weil der Ausgang eines
LinCMOS-Opamp nicht symmetrisch maximal ausgesteuert werden kann, darf
Ux nicht auf der halben Betriebsspannung liegen, weil im Falle einer
Übersteuerung die postive Ausgangsamplitude stärker beschnitten
(geklippt) wird als die Amplitude in GND-Nähe. Die Ausgangsspannung Ua
könnte den maximal möglichen Wert gar nicht erreichen, wenn Ux = Ub/2.
Man beachte den Kasten Ua (Ua = Ausgangsspannung). Bei der
vorliegenden Betriebsspannung von 6 VDC ist eine Aussteuerung von
maximal etwa 5 V möglich. Eine Amplitudenbegrenzung erfolgt am Ausgang
also dann symmetrisch, wenn die Spannung Ux auf 2.5 VDC und nicht auf
der Hälfte der Betriebsspannung von 3 VDC liegt. Mit den zwei
Ux-bestimmenden einprozentigen Widerständen R6 und R7 hat Ux einen Wert
von 2.57 VDC. Für den Ux-Spannungswert bei anderen Betriebsspannungen
konsultiere man das Datenblatt des TLC271 (Datenblatt-Link weiter oben).
Es gelten die Diagramme "High-Level Output Voltage vs Supply
Voltage". C4 dient der Dämpfung von allfälligen Stör- und
Rauschspannungen, weil R6 und R7 relativ hochohmig sind. Diese
Hochohmigkeit macht besonders dann Sinn, wenn Lowpower-Opamps im Spiel
sind, damit auch der Querstrom durch R6 und R7 ebenfalls niedrig ist
(Batterieanwendung). C5 sorgt dafür, dass die Quellimpedanz von Ux auch
im mittelfrequenten Bereich sehr niederohmig bleibt. Dynamisch
betrachtet, entspricht die Impedanz dem Wert von GND. Bei
höherfrequenten Anwendungen müsste man zum Elko C5 ein induktionsarmer
Keramikkondensator von etwa 100 nF parallel schalten. Dies erübrigt sich
meist, weil solche Kondensator in der Regel nahe bei der IC-Speisung
eingesetzt werden.
Die Verstärkerschaltung ist mit zwei kleinen Unterschieden die selbe von
Bild 6. Jeder Verstärkerteil enthält zusätzlich parallel zum
Gegenkopplungswiderstand R2 bzw. R5 ein Kondensator C1 bzw. C2. R2
bildet mit C1 und R5 bildet mit C2 je ein einfaches Tiefpassfilter
erster Ordnung. Da diese beiden Tiefpassfilter mit den Teilverstärkern
in Serie geschaltet sind, wird die Grenzfrequenz des einzelnen
Tiefpassfilters auf den Dämpfungswert von 1.5 dB und nicht wie gewohnt
auf 3 dB berechnet. Die Formel dazu steht links im Kasten. Unten rechts
sieht man das typische Bodediagramm, das sogleich zeigt, dass die
Übertragung im Durchlassbereich ziemlich nichtlinear ist. Ebenso zeigt
dies die oben liegende kleine Tabelle. Weil es im Ganzen betrachtet ein
Tiefpassfilter zweiter Ordnung ist, beträgt die maximale Steilheit im
oberen Grenzfrequenzbereich 12 dB/Oktave. Man muss noch beachten, dass
diese Methode der Tiefpassfilterung nur dann ihre Wirkung zeigt, wenn
die Verstärkung pro Verstärkerteil nicht zu niedrig gewählt wird, weil
kleiner als 1 (0 dB) kann die Verstärkung nicht werden.
Es muss bei dieser Schaltung klar erkannt werden, dass eine solche
Vereinfachung von Verstärker und Filter sich nicht oder nur selten für
messtechnische Aufgaben eignet. Die Nichtlinearität ist im nutzbaren
Frequenzbereich einfach zu gross. Sehr wohl eignet sich eine solche
Vereinfachung z.B. für die
EMG-Biofeedback-Anwendung,
bei der es bloss auf einen Spannungsmittelwert ankommt, der in ein
akustisches oder optisches Signal umgesetzt wird.