Operationsverstärker III:
Die virtuelle Spannung, noch einmal...
und der Einschwingvorgang
Einleitung
Dieser Elektronik-Minikurs Operationsverstärker III erweitert
Operationsverstärker I im
Themenbereich virtuelle Spannung und virtueller GND. Während in
Operationsverstärker I
diese Virtualiät eher beiläufig zu praktischen Grundschaltungen
thematisiert wird, ist sie im ersten Kapitel "Wie kommt es zum
virtuellen GND und zur virtuellen Spannung?" in diesem
Elektronik-Minikurs sehr zentral. Der Inhalt ist hier differenzierter
und trotzdem anschaulich beschrieben. Dieses Kapitel wurde mit dem
Update vom Juni 2010 hinzugefügt.
Um dem Verständnis betreffs virtuelle Spannung/GND eine zusätzliche
Chance zu geben, wird diese Problematik im ersten Kapitel aus einer
etwas andern Perspektive erläutert. Praktische Versuche, die jeder
selbst durchführen kann, zeigen, wo die Grenzen des virtuellen GND bzw.
der virtuellen Spannung sind. Dabei wird aufgezeigt, dass die virtuelle
Spannung oder der virtuelle GND eine direkte Auswirkung der sehr hohen
Leerlaufverstärkung (Open-Loop-Gain) des Operationsverstärker ist.
Zu den weiteren Kapiteln: Wir betrachten die virtuelle Spannung beim
Impedanzwandler (Verstärkung = 1), gehen weiter zum gegengekoppelten
Operationsverstärker, der die Eingangsspannung verstärkt und setzen fort
mit einem Leistungs-Operationsverstärker, bei dem zwischen seinem
Ausgang und dem Anschluss einer Last (je nachdem Lautsprecher, Motor,
Heizung etc.) der Leitungswiderstand berücksichtigt werden muss, wobei
das Gegenkopplungsnetzwerk bei der Lastspannung und nicht am Ausgang des
Operationsverstärkers angeschlossen sein muss. Bei all dem konzentrieren
wir uns auf die virtuelle Spannung am nichtinvertierenden Eingang.
Das zweite Thema befasst sich ebenfalls mit einer Fortsetzung aus
Operationsverstärker I. Es geht
um die Geschwindigkeit des Operationsverstärkers (Unity-Gain-Bandbreite
und Slewrate), wobei uns hier das Einschwingverhalten interessiert. Es
geht darum zu verstehen was am Ausgang passiert, wenn am Eingang eine
steile Impulsflanke auftritt und wie sich die virtuelle Spannung bzw.
die Differenzspannung am Eingang des Operationsverstärkers
verhalten.
Wie kommt es zum virtuellen GND und zur virtuellen Spannung?
Bevor wir uns dieser Frage widmen, wollen wir erkennen was unter
Virtualität generell verstanden wird. Dazu bitte ich das einleitende
Kapitel Virtualität im
Wikipedia zu lesen.
Interessant ist der erste Satz im zweiten Abschnitt, hier wiedergegeben:
- Virtualität spezifiziert also eine gedachte oder über ihre Eigenschaften konkretisierte Entität, die zwar nicht physisch, aber doch in ihrer Funktionalität oder Wirkung vorhanden ist. Somit ist "virtuell" nicht das Gegenteil von "real" - obwohl es fälschlicherweise oft so verwendet wird - sondern von "physisch".
Bezogen auf die virtuelle Spannung (bzw. virtuellem GND) bedeutet dies, dass diese der Funktionalität der physikalisch echten Spannung entspricht, allerdings nur in gewissen Grenzen. Diese Grenzen wollen wir kennen lernen. Bild 1 erklärt die Eigenschaft des virtuellen GND am praktischen Beispiel, das zum eigenen Experimentieren einlädt. Die Unterschiede werden so leicht deutlich. Mit elektrischem GND (Ground) ist die elektrische Masse gemeint.
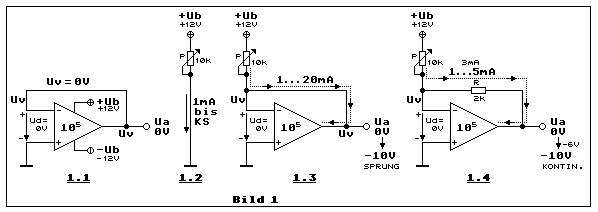
Teilbild 1.1 stellt die einfachste Form einer Verstärkerschaltung mit
einem Opamp dar. Wegen der vollständigen Gegenkopplung durch die direkte
Verbindung vom Ausgang Ua zum invertierenden Eingang, beträgt die
Verstärkung 1. Ua = Uv (v = virtuell) und Ud = 0 VDC. Ud ist immer 0 VDC
im eingeschwungenen Zustand des Opamp in der Funktion als
gegengekoppelter Verstärker. Das gilt für die Verarbeitung/Verstärkung
von DC- und AC-Spannungen bei niedrigen Frequenzen. Da bei diesen
Experimenten DC-Spannungen verwendet werden, erfolgen die
Spannungsangaben hier im Text in VDC.
Teilbild 1.2 zeigt ein Leistungs-Potmeter, beschaltet zwischen +Ub = 12
VDC und GND. Ist P auf seinen maximalen Widerstand eingestellt, fliesst
ein Strom von 1.2 mA. Ist P auf Null Ohm eingestellt, ist Kurzschluss
(KS). Verwendet man für dieses einfache Experiment ein Netzgerät mit
einer einstellbaren Strombegrenzung und man stellt diese auf einen Strom
von 1 A ein, fliesst zwischen +Ub und GND ebenso 1 A. Das ist eigentlich
so einfach und logisch, dass man es gar nicht erst erwähnen muss, ginge
es nicht um den Vergleich mit der Funktion des echten GND zum virtuellen
GND in Teilbild 1.3.
In Teilbild 1.3 wird am invertierenden Eingang auf die selbe Art der
virtuelle GND erzeugt wie in Teilbild 1.1. Wir setzen auch hier in
Teilbild 1.3 das selbe Leistungs-Potmeter P ein und beginnen damit
seinen Widerstand zu reduzieren. Gleichzeitig messen wir die Spannung
Ud, Uv oder Ua, was hier auf das selbe rauskommt. Wir erhöhen den Strom
bis auf fast 20 mA und stellen fest, dass der virtuelle GND Uv seine
Pflicht erfüllt. Wir messen 0 VDC. Wir erhöhen den Strom weiter und
weiter und plötzlich verweigert der virtuelle GND seinen Dienst. Die
drei identischen Spannungen Uv, Ud und Ua steigen mit gleicher Spannung
an. Je niederohmiger wir den Widerstand von P einstellen, um so höher
werden Uv, Ud und Ua. Bei P = 0 Ohm sind es +12 VDC. Der Strom selbst
stabilisiert sich bei etwa 20 mA oder etwas mehr. Was passiert da? Ganz
einfach, die integrierte Endstufe des Opamp wird überfordert und die
ebenfalls integrierte Strombegrenzung setzt ein und begrenzt zum Schutz
des Opamp den Strom zum Ausgang des Opamp. Dieser Begrenzungsstrom von
20 mA ist ein Beispiel und orientiert sich nicht an einen bestimmten
Opamp-Typen.
Fazit: Die virtuelle Spannung, die hier das Potenzial des GND
hat, wird durch den Opamp regeltechnisch erzeugt, solange er korrekt
arbeitet. Darunter versteht sich, dass die extrem hohe Opamp-interne
Leerlaufverstärkung (Open-Loop-Gain) wirken kann. Obwohl eine
vollständige Gegenkopplung mit einer Verstärkung von 1
(Closed-Loop-Gain) vorliegt, ist für die Bildung der Virtuellen Spannung
oder des virtuellen GND nur die sehr hohe Leerlaufverstärkung
(Open-Loop-Gain) zuständig! Mehr dazu folgt weiter unten mit Bild 2.
Teilbild 1.4 unterscheidet sich von Teilbild 1.3 nur durch den
eingebauten Widerstand R mit einem Wert von 2 k-Ohm im
Gegenkopplungspfad. Hier passiert etwas anderes, wenn wir den Strom
erhöhen. Bei Stromwerten unterhalb von 5 mA (nur ein Beispiel) erfüllt
der virtuelle GND seine Pflicht. Uv und Ud = 0 VDC. Die Ausgangsspannung
erhöht sich auf einen negativen Wert in dem Masse wie man den Strom
durch R2 erhöht. Wie kommt das? Ganz einfach, der Strom der durch R2
fliesst, erzeugt an R eine Spannung. Der Strom fliesst dabei von +Ub
über P und R in den Eingang des Opamp. Weil Ud und Uv = 0 VDC, muss die
Spannung an Ua zwangsläufig negativ sein. Bei einem Strom von 3 mA
liegen über R 6 VDC und diese selbe Spannung liegt an Ua mit -6 VDC.
Erhöhen wir den Strom weiter bis 5 mA, ist das Ende der Fahnenstange
erreicht und der virtuelle GND versagt seinen Dienst. Grund dafür ist
der, dass die Endstufe nicht in der Lage ist eine höhere negative
Ausgangsspannung zu liefern, als diese -10 VDC. Erhöht man den Strom
weiter, geht das, bis die Opamp-interne Strombegrenzung anspricht. Dabei
erhöhen sich Uv und Ud gleichermassen. Der Opamp arbeitet nicht mehr
richtig. Auch hier sind die genannten Begrezungswerte nur Beispiele. Es
gibt typenbedingte Abweichungen. Aber die Werte sind im realistischen
Bereich. Da dieser Opamp an ±Ub mit ±12 VDC spannungssymmetrisch
gespiesen wird, ist eine ausgangsseitige Maximalspannung (Ua) von etwa
±10 VDC typisch, ausser es ist ein moderner sogenannter
Rail-to-Rail-Opamp, dessen Ausgang bis zur positiven und negativen
Betriebsspannung ausgesteuert werden kann, sofern der Ausgang nur wenig
belastet ist.
In den Opamps sieht man die Zahl 100'000 als 105 eingetragen.
Das deutet auf die typisch sehr hohe Leerlaufverstärkung eines jeden
Opamps hin. Dieser Wert ist in der Grössenordnung realistisch, trotzdem
aber nur ein Beispiel. Ich weise an dieser Stelle darauf hin, dass
derart hohe Leerlaufverstärkungen nur bei der Verarbeitung von
DC-Spannungen und AC-Spannungen mit sehr niedrigen Frequenzen gelten.
Bei höheren Frequenzen ist diese Leerlaufverstärkung entsprechend
niedriger. Mehr dazu, weiter unten mit Bild 5 und im Kapitel
"Leerlaufverstärkung, Differenzspannung und Frequenz" in
Operationsverstärker I.
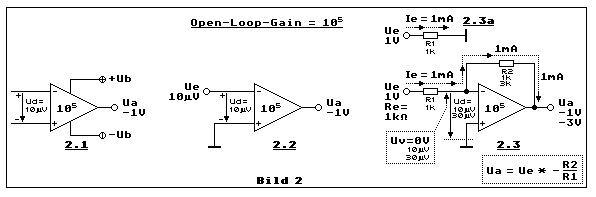
In Bild 2 geht es darum zu erkennen, wie es zum virtuellen GND kommt und
es geht um zusätzliche Realität dieser Virtualität. Dies erkennt man
daran, dass jetzt Spannungswerte im µV-Bereich zwischen den beiden
Opampeingängen zum Ausdruck kommen. Dies ist auch das Thema in
Verbindung mit Bild 3 und Bild 4.
Teilbild 2.1 zeigt dies am einfachsten Beispiel. Der Opamp ist nichts
anderes als ein Verstärker, der mit seinen beiden Eingängen in der Lage
ist, differenzielle Eingangsspannungen zu verstärken. Die meisten Opamps
liefern die verstärkte Spannung an einen asymmetrischen Ausgang, dessen
Ausgangsspannung sich auf GND bezieht. Es gibt nur wenige Opamps mit
differenziellen Ausgängen. Wenn der Ausgang Ua z.B. eine Spannung von -1
VDC anzeigt, dann beträgt differenzielle Eingangsspannung, wegen der
sehr hohen Leerlaufverstärkung von z.B. 100'000, gerade 10 µVDC. Ist Ua
fast maximal so gross wie die positive oder negative Betriebsspannung
des Opamp, beträgt Ud kaum mehr als 0.1 mVDC. Man kann daher
praxisbezogen aussagen, dass Ud praktisch Null Volt ist, unabhängig
davon wie gross Ua ist. Nennen wir dies die Volt-Perspektive.
Teilbild 2.2 zeigt das selbe wie Teilbild 2.1 mit dem Unterschied, dass
der nichtinvertierende Eingang mit GND verbunden ist. Dadurch gibt es
nur einen Eingang Ue der zum nichtinvertierenden Eingang des Opamps
führt. Ue ist gleich gross wie Ud. Praktisch gesehen 0 VDC.
Aus Teilbild 2.2 wird Teilbild 2.3 mit der Eigenschaft einer
invertierenden Verstärkerschaltung, dessen (äussere) Verstärkung
praktisch alleine durch das Gegenkopplungsnetzwerk aus R1 und R2
besteht. Die Berechnungsformel ist sehr einfach. Obwohl in der Skizze
vermerkt, interessiert sie uns hier nicht. Wir wollen alleine durch das
Nachvollziehen der einfachen Schaltung verstehen, wie sie arbeitet.
Wir wissen nun, gleichgültig wie klein oder wie gross Ua innerhalb des
zulässigen Spannungsbereiches, gegeben durch ±Ub, ist, Ud hat stets den
praktischen Wert von 0 VDC. Wir legen an Ue eine DC-Spannung von 1 VDC.
Weil der Widerstand R1 ein Wert von 1 k-Ohm hat, fliesst zum Knoten beim
invertierenden Eingang ein Strom von 1 mA. Der Strom, der zum Knoten
fliesst, muss auch wieder wegfliessen
(Knotenregel)
und da gibt es nur eine Richtung. Der Strom von 1 mA fliesst durch den
Widerstand R2 in den Ausgang (Endstufe) des Opamp. Und weil der
Widerstand R2 ebenfalls 1 k-Ohm aufweist, fällt an R2 eine Spannung 1
VDC ab. Weil der Knoten virtuell auf 0 VDC (GND-Pegel) liegt und der
Strom von dort wegfliesst, wird Ua mit -1 VDC zwangsläufig negativ. Aber
warum bleiben Uv und Ud praktisch 0 VDC? Ganz einfach: Zwischen den
beiden differenziellen Eingängen und dem Ausgang des Opamp gilt die
(innere) sehr hohe Leerlaufverstärkung. Im vorleigenden Beispiel
100'000. Das bleibt auch so wenn man die gegengekoppelte Verstärkung
(Closed-Loop-Gain) verändert. Hier auf den Wert von -3 mit der Änderung
des R2 von 1 k-Ohm auf 3 k-Ohm. Ua erhöht seine negative Spannung von -1
VDC auf -3 VDC. Dabei ändert sich Uv bzw. Ud von 10 µVDC auf 30 µVDC.
Die Funktion des virtuellen GND beim Knoten des invertierenden
Einganges, der rein regelungstechnisch durch die sehr hohe
Leerlaufverstärkung zustande kommt, bleibt erhalten, wenn der Opamp
nicht überfordert wird. Der Strom, der vom Knoten in den invertierenden
Eingang fliesst, gilt hier und in der Regel als vernachlässigbar klein.
Die Grösse des Eingangswiderstandes Re am Eingang Ue: Was
unterscheidet der virtuelle GND vom echten GND. Ganz praktisch gesehen,
nichts. Wir betrachten die kleine Skizze 2.3a. Der selbe Widerstand der
in der Opampschaltung (Teilbild 2.3) Ue mit dem virtuellen GND
verbindet, verbindet in der Skizze 3.2a Ue mit dem echten GND. In beiden
Anwendungen fliesst ein Strom von exakt 1 mA. Und deshalb entspricht bei
beiden Anwendungen der Eingangswiderstand Re dem Wert von R1 und das
sind 1 k-Ohm. Es ist falsch, wenn man annimmt, dass Re der Summe von R1
und R2 entspricht. Das wäre dann der Fall, wenn die Spannung am Knoten
des invertierenden Eingangs sich proportional einer Spannungsänderung
von Ue anpasst. Aber dem ist nicht so!
Das ist am Anfang des Opampstudiums verwirrend. Man fragt sich, warum
ist das so, schliesslich fliesst in den virtuellen GND keinen Strom
hinein, beim echten GND aber schon. Der Strom fliesst ja weiter über R2
in den Ausgang des Opamp. Das stimmt, aber während der (äusseren)
Verstärkung, welche durch die Gegenkopplung mit R1 und R2 zustande
kommt, regelt die extrem hohe (innere) Leerlaufverstärkung, die
differenzielle Eingangsspannung Ud auf wenige zehn Mikrovolt. Der
virtuelle GND unterscheidet sich vom echten nur darin, dass der
virtuelle einen sehr kleinen DC-Offset im 10-µV-Bereich aufweist,
während der echte GND knallhart 0 VDC hat. Stimmt das wiklich? Nein
keineswegs, auch die Kontaktierung mit einem echten GND kann leicht,
wegen seinem begrenzten Widerstand und wegen sogenannten
Thermopannungen, DC-Offsetwerte im 10-µV-Bereich aufweisen. Rein
funktionell betrachtet besteht kein Unterschied. Für beide Arten von GND
gilt die Bedingung "im zulässigen Arbeitsbereich". Dieser ist beim
echten GND ganz einfach wesentlich grosszügiger. Für den virtuellen und
für den echten GND gilt, dass beide extrem niederohmig sind. Beim
virtuellen GND kommt dies regelungstechnisch zustande und das bedeutet,
dass dies im eingeschwungenen Zustand gilt.
Es war soeben von DC-Offsetspannungen die Rede. Diese angegebenen Werte
beziehen sich auf das vorliegende Beispiel. In Wirklichkeit gibt es
weitere systembedingte DC-Offsetspannungen. Um darüber mehr zu erfahren,
konsultiere man
Operationsverstärker I und
Operationsverstärker II.
Die Opampschaltung bietet zwei Verstärkungsmöglichkeiten, entweder
Verstärkung -1 (R2 = 1 k-Ohm) oder -3 (R2 = 3 k-Ohm). Weil die extrem
hohe (innere) Leerlaufverstärkung nicht unbegrenzt hoch ist, erhöht sich
Differenzspannung Ud, und somit die virtuelle Spannung Uv auf 30 µVDC.
Aus der Volt-Perspkektive betrachtet, ändert sich also nichts daran,
dass der virtuelle GND mit einer Spannung von 0 VDC gewährleistet ist.
Der Strom Ie = 1 mA bleibt der selbe und daraus resultiert im
Nebeneffekt eine neue Erkenntnis: Die invertierende Verstärkerschaltung
ist auch eine Konstantstromquelle zwischen dem virtuellen GND Uv und Ua,
weil der Strom durch die Veränderung des Widerstandes R2 unverändert
bleibt, sofern Ua nicht an den Limit gerät.
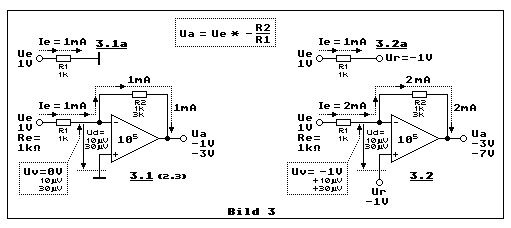
Vom virtuellen GND zur virtuellen Spannung: Teilbild 3.1 ist die
exakte Wiedergabe von Teilbild 2.3. Diese Schaltung ist in Teilbild 3.2
einzig dadurch erweitert, dass der nichtinvertierende Eingang des Opamp
nicht mit dem GND als Referenzspannung mit 0 VDC, sondern mit -1 VDC
verbunden ist. Diese Referenzpannung Ur von -1 VDC dient nur als
Beispiel. Es kann auch eine andere Spannung sein, die auch positiv sein
darf. An diesem Beispiel in Teilbild 3.2 soll gezeigt werden, was sich
betreffs virtueller Spannung gegenüber der Schaltung in Teilbild 3.1
ändert.
Wir wissen jetzt, wie hoch die Ausgangsspannung Ua auch ist, die
(innere) Leerlaufverstärkung ist so gross, dass die Differenzspannung Ud
etwa im 10-µV-Bereich bleibt. Das bedeutet nichts anderes, die virtuelle
Spannung am invertierenden Eingang des Opamp ist praktisch gleich gross
wie Ur. Im vorliegenden Beispiel -1 VDC. Ue, R1 und R2 sind gleich gross
wie in Teilbild 3.1. Das bedeutet, dass zwischen Ue und der virtuellen
Spannung Uv 2 VDC liegen und dies erzeugt durch R1 mit 1 k-Ohm einen
Strom von 2 mA. Diese 2 mA fliessen in den Ausgang des Opamp (Endstufe)
und erzeugen über R2, mit ebenfalls 1 k-Ohm, eine Spannung von 2 VDC.
Diese Spannung muss von der virtuellen Spannung subrahiert werden. Das
Resultat davon ist die Ausgangsspannung Ua von -3 VDC. Erhöht man R2 auf
3 k-Ohm beträgt Ua -7 VDC.
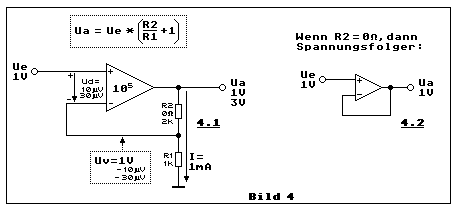
Zur Untersuchung des virtuellen GND und der virtuellen Spannung diente
bisher die invertierende Verstärkerschaltung. Jetzt untersuchen wir
diese Virtualität an der nichtinvertierenden Verstärkerschaltung, gemäss
Bild 4. Im Grunde ändert sich nichts, ausser dass wir es hier ständig
mit einer virtuellen Spannung Uv zu tun haben. Uv hat den selben Wert
wie Ue, ist jedoch virtuell. Wenn R2 = 0 Ohm, haben wir es mit dem
Spannungsfolger bzw. Impedanzwandler zu tun, wie dies Teilbild 4.2
zeigt. Der Strom I vom Ausgang des Opamp nach GND ergibt sich aus Uv/R1.
Im vorliegenden Beispiel ergibt das 1 mA. Auch hier, wir haben es
zwischen dem Opampausgang und der virtuellen Spannung mit einer
Konstantstromquelle zu tun - sofern Ue auf einen konstanten Wert
eingestellt ist. Diese Konstantstromquelle bewirkt eine proportionale
Abhängigkeit der Spannung über R2 von der Grösse R2.
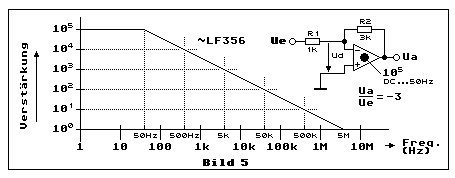
Bild 5 zeigt den Frequenzgang eines Bodediagrammes. Der Phasengang
wäre dann nötig, wenn man genau in die Details gehen möchte. Um das
Thema der differenziellen Eingangsspannung Ud und der virtuellen
Spannung, bzw virtuellen GND, abzurunden, genügt diese Ausführung.
Der Frequenzganz des Diagrammes ist typisch für den berühmten Opamp
LF356
von NSC. Die Frequenzbandbreite bei Verstärkung 1 (Unity-Gain) liegt bei
5 MHz. Das bedeutet im praktischen Beispiel, dass die Frequenzbandbreite
von 5 kHz gerade noch bei einer Verstärkung von 1000 eingehalten wird.
Bei 10'000 sind es gerade noch 500 Hz und bei 100'000 noch 50 Hz.
Unterhalb dieser Frequenzbandbreite bis zu 0 Hz (DC), ist eine
Verstärkung von 100'000 möglich. Bei all diesen Verstärkungsangaben
haben wir es mit der Verstärkung zu tun, welche sich aus der (äusseren)
Gegenkopplung mit R1 und R2 (andere Werte) ergibt. Allerdings, bei
100'000 gibt es diese Gegenkopplung gar nicht mehr, weil nämlich diese
Verstärkung der (inneren) Leerlaufverstärkung entspricht. Praktisch ist
diese hohe Verstärkung nicht anwendbar, weil, ohne jede Gegenkopplung
ist die Verstärkung nicht allzu linear und es haften ihr weitere
Ungenauigkeiten an, wie z.B. die Temperaturabhängigkeit. Was uns hier
aber speziell interessiert, ist die Spannung Ud.
Wenn der Opamp mit einer Verstärkung von z.B. 3 oder -3 bei DC bis 50 Hz
arbeitet, liegt Ud im 10-µV-Bereich. Bei einer Frequenz von 50 kHz
jedoch im 10-mV-Bereich. Aus der Volt-Perspektive betrachtet, kann man
schon fast nicht mehr von einem virtuellen GND Uv oder von einer
virtuellen Spannung reden. Je höher die Signalfrequenz an Ue ist, um so
niedriger ist das Verhältnis von der Eingangsspannung Ue zur
Differenzspannung Ud, weil die Leerlaufverstärkung niedriger ist. Diese
Dämpfung ergibt sich aus der Frequenzgangkompensation. Ohne die kann ein
Opamp nicht stabil arbeiten. Mehr dazu in
Vom Operationsverstärker bis zum
Schmitt-Trigger.
Schlusswort zum ersten Kapitel: Die weiteren Kapitel sind älter
als das erste. Man erkennt dies leicht in der Gestaltung der
Schaltschemata, die ein wenig anders sind. Im Gegensatz zu den
bisherigen Bildern, sind die Spannungswerte, die als Beispiele dienen,
kleiner geschrieben. Betreffs virtuellem GND und virtueller Spannungen
gibt es inhaltlich gewisse Wiederholungen, die aber sehr viel kürzer und
drastisch weniger differenziert sind. Genau das ist schliesslich auch
die Ursache für das neue erste Kapitel (Juni 2010).
Die virtuelle Spannung vom Impedanzwandler bis zum Verstärker
bei der nichtinvertierenden Verstärkerschaltung
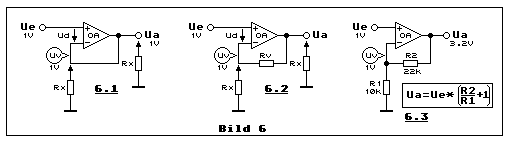
Der vollständig gegengekoppelte Opamp, der Impedanzwandler mit seiner
typischen Verstärkung von 1, hat eine direkte Verbindung vom Ausgang zum
invertierenden Eingang des Opamps. Ua und die virtuelle Spannung Uv sind
identisch. Es kommt also auf das selbe heraus, ob man einen beliebigen
nicht allzu niederohmigen Widerstand Rx (z.B. 1 k-Ohm) an Ua oder an Uv
anschliesst. Die Spannung über Rx bleibt gleich, weil die
Differenzspannung Ud im eingeschwungenen Zustand des Opamp stets fast 0
V (DC oder AC sehr niederfrequent) ist.
Fast bedeutet, dass Ud abhängig ist vom Verhältnis der gegengekoppelten
Verstärkung zur Leerlaufverstärkung und damit auch abhängig ist von der
Signalfrequenz an Ue, wie dies bereits weiter oben und in
Operationsverstärker I
erklärt ist. Wir haben es hier einfachheitshalber mit DC-Spannungen
(Frequenz = 0 Hz) zu tun, weshalb hier Ud mit der Spannung VDC
gezeichnet wird. Weiter beschäftigen wir uns nur mit sehr niedrigen
Verstärkungsfaktoren, die durch die äussere Gegenkopplung bestimmt
sind. Die Leerlaufverstärkung ist dabei extrem hoch. Bei einem Opamp
des Typs LF356 beträgt sie 106 dB, das einem Faktor von 200'000
entspricht. Alleine diese hohe Leerlaufverstärkung ist praktisch
verantwortlich dafür, dass Ud praktisch 0 VDC ist. Einfachheitshalber
sind hier alle Beispiele auf 100'000 (100 dB) bezogen.
Ue ist im Beispiel in Bild 6 auf 1 VDC eingestellt. Extrem betrachtet
und gemessen mit einem hochauflösenden digitalen Voltmeter, wird man
feststellen, dass Ua geringstfügig grösser ist als Uv bzw. Ue, wenn Rx
an Uv und nicht an Ua angeschlossen ist, weil die Verbindung vom Ausgang
zum invertierenden Eingang nicht exakt Null Ohm hat. Diese
verlustbehaftete Verbindung ist mit Rv (Verlustwiderstand)
gekennzeichnet. Uv entspricht Ue und Ua addiert sich aus Uv plus dem
Spannungsabfall über Rv. Damit lernen wir mit Teilbild 6.2 etwas Neues:
Der Opamp führt seinen Regelprozess auch dann aus, wenn zwischen seinem
Ausgang und dem Verbraucher (Rx), wo die Gegenkopplung ansetzt, eine
verlustbehaftete Leitung liegt. Ud bleibt auch so 0 VDC und die Spannung
Uv bleibt unverändert. Genau nach diesem Prinzip arbeitet, nebenbei
erwähnt, eine hochstabile geregelte DC-Spannungsquelle, wenn die
Gegenkopplung nicht am Ausgang des Netzteiles, sondern direkt am
Verbraucher ansetzt. Solche Netzteile haben für eine solche
Feedbackmethode zusätzlich spezielle Sense-Anschlüsse.
Mit dieser Betrachtung befinden wir uns auf dem Weg zum
nichtinvertierenden Verstärker in Teilbild 6.3 und da sehen wir im
Prinzip das selbe Schaltbild wie in Teilbild 6.2. Der einzige
Unterschied besteht darin, dass aus Rv und Rx, R2 und R1 wurde. Mit R2 =
22 k-Ohm und R1 = 10 k-Ohm wird Ue = 1 VDC auf Ua = 3.2 VDC verstärkt.
Die Berechnung erfolgt nach angegebener Formel. Auch hier gilt, dass Ud
= 0 VDC, unabhängig davon wie stark man R1 oder/und R2 verändert. Die
Summe von R2 und R1 darf nur nicht so stark unterschritten werden, dass
der Strom bei entsprechender Ausgangsspannung Ua zu gross wird und der
Opamp die Ausgangsspannung begrenzt (Clipping). Das ist je nach Typ des
Opamp sehr unterschiedlich. Mehr Information dazu liefert das
entsprechende Datenblatt. Man muss natürlich auch noch darauf achten,
dass die Ausgangsspannung Ua im zulässigen Bereich liegt, der von der
Betriebsspannung diktiert wird. Nur innerhalb dieses Bereiches kann Ud =
0 VDC erfüllt werden.
Betrachtungen mit einem Leistungs-Opamp
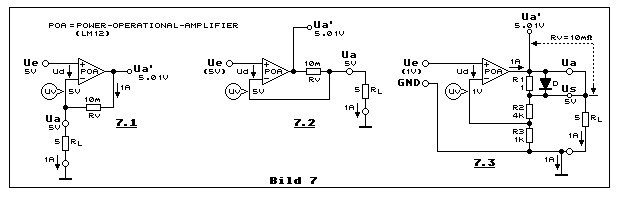
Wir betrachten hier die Situation mit Uv bei der Anwendung eines
Leistungs-Opamp. Ich verwendete vor sehr langer Zeit den LM12 für den
Bau einer Audio-Leistungsendstufe. Es kann aber ebenso gut ein
gewöhnlicher Opamp sein, der mit einer diskreten komplementären
Transistorstufe erweitert ist und die Gegenkopplung über die ganze
Schaltung wirkt. Eine solche Schaltung ist in
(4) beschrieben.
Diese Leistungsverstärkerstufe nennen wir POA für
Power-Operational-Amplifier oder abgekürzt Power-Opamp.
Teilbild 7.1 ähnelt Teilbild 6.2 mit Rx an Uv angeschlossen. Rv ist auch
hier der Verlustwiderstand der Leitung zwischen Ausgang Ua' des POA und
der Last an Ua. Als realistischer Wert setzen wir für Rv 10 m-Ohm ein.
Irgendwie befremdet es, dass der Lastwiderstand RL,
hier mit einem Widerstand von 5 Ohm, an der virtuellen Spannung Uv
angeschlossen ist. So was schliesst man doch am Ausgang des POA an.
Welch eine verkehrte Welt der Elektronik! Es sollte einem aber stutzig
machen, wenn man etwas genauer hinsieht. Rv hat einen Wert von nur 10
Milli-Ohm und die Bezeichnung Ua ist identisch mit Uv und dort wo
normalerweise Ua ist, ist Ua' gezeichnet und die Spannung an Ua' ist um
den Wert des Spannungsabfalles über Rv geringfügig höher. Man beobachte
auch den Weg des Laststromes, hier 1 A.
Wir kommen zu Teilbild 7.2, wobei diese Schaltung exakt identisch ist
mit der in Teilbild 7.1. Der Unterschied besteht bloss darin, dass die
Schaltung in Teilbild 7.2 so gezeichnet ist, dass sie keine Verwirrung
mehr anstiftet. Die Welt der Elektronik ist damit wieder in Ordnung. Nun
sie ist es eigentlich auch mit Teilbild 7.1, aber Teilbild 7.2 ist
anschaulicher und es leuchtet sofort ein, was mit Rv mit seinem sehr
niedrigen Ohmwert gemeint sein könnte. Es ist der Verlustwiderstand der
Leitung zwischen dem Ausgang POA Ua' und der Last, angeschlossen an Ua.
Die Gegenkopplung wird nach dieser verlustbehafteten Zuleitung in der
Nähe des Verbrauchers RL vorgenommen und so
garantiert man an Ua eine besonders lastunabhängige konstante Spannung,
weil Uv mit Ue schliesslich (fast) identisch ist, und Uv = Ua, weil die
Verstärkung durch maximale Gegenkopplung 1 (0 dB) beträgt.
Teilbild 7.3 erweitert die Schaltung von Teilbild 7.2 in einen
Leistungsverstärker mit einer nichtinvertierenden Verstärkung von 5,
gegeben durch das Gegenkopplungsnetzwerk von R2/R3. Us ist die
sogenannte Sensorspannung, bei der die Gegenkopplung direkt an den
Verbraucher geschaltet wird. R1, mit einem sehr viel kleineren
Widerstand als R2 oder R3, dient einzig dazu, dass die geregelte
Spannung an Ua einigermassen aufrechterhalten wird, wenn der Verbraucher
RL (noch) nicht auch an Us angeschlossen ist. Diode
D schützt R1 vor zu hoher Leistung, wenn Ua zuerst und danach Us im
Betriebszustand getrennt wird, in dem die Spannung über R1 durch D
begrenzt wird. Genau mit solchen Methoden arbeitet man beim Entwurf
hochwertiger und hochpräziser analoger Netzteile und Netzgeräte. Man
denkt bei solch einer Schutzmassnahme auch ein wenig in der Richtung,
dass der Anwender nicht immer so ganz seriös mit einem Gerät umgeht,
wie es eigentlich sein sollte. Betriebsanleitungen werden oft erst dann
gelesen, wenn die ersten Rauchzeichen aufsteigen...
Kommen wir zurück zur virtuellen Spannung Uv. Welchen Wert die
Verstärkung, definiert mit R2/R3 auch hat, Uv bleibt konstant auf dem
Wert von Ue. Es gelten auch hier ganz genau die selben Betrachtungen
betreffs extrem hoher Leerlaufverstärkung, wie bereits gehabt. Aber da
wir es hier mit hohen Strömen zu tun haben, sei noch darauf hingewiesen,
dass der GND von RL so mit dem GND der
Spannungsquelle Ue verbunden sein muss, dass über diese GND-Leitung kein
Last-Teilstrom fliesst, denn sonst entsteht eine sogenannte
GND-Rückkopplung (GND-Loop) die leicht zu Instabilität und zu
Schwingungen führt. Man beachte den Strompfeil mit der Angabe von 1
Ampere (1A) als Beispiel. Dies ist ein alt bekanntes Problem beim Bau
von analogen Netzteilen, Audio-Leistungsverstärkern und anderen analogen
Last-Regelschaltungen. Man beachte die GND-Verbindung zwischen Ue und
Anschluss von RL. So ist diese GND-Leitung im
Signalpfad sicher laststromfrei.
Die virtuelle Spannung vom Impedanzwandler bis zum
Verstärker bei der invertierenden Verstärkerschaltung
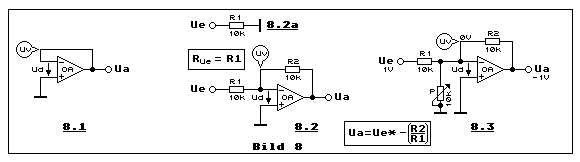
Teilbild 8.1 zeigt wiederum den typischen Impedanzwandler mit
Verstärkung 1, wie er in Teilbild 6.1 abgebildet ist. Der einzige
Unterschied besteht in Teilbild 8.1 darin, dass der nichtinvertierende
Eingang mit GND verbunden ist. Wir wissen jetzt auch, dass die virtuelle
Spannung Uv praktisch dem GND-Pegel entspricht, weshalb man in diesem
Fall Uv auch als virtuellen GND bezeichnet. Dass die Schaltung in
Teilbild 8.1 kaum einen Nutzen hat, leuchtet ein. Sie dient auch nur zur
Anschauung für den nächsten Schritt in Teilbild 7.2, der typischen
invertierenden Verstärkerschaltung.
Wie die Spannung Ud = 0V zustande kommt, wissen wir. In dieser Hinsicht
ändert sich in Teilbild 8.2 nichts. Diese Tatsache hat zur Folge, dass
der Eingangswiderstand an Ue exakt dem Wert von R1 entspricht. Das kommt
praktisch auf das selbe heraus, als ob Ue über R1 direkt mit GND
verbunden ist, wie dies Teilbild 8.2a illustriert. Auch das ist weiter
oben bereits differenzierter beschrieben und an dieser Stelle bekannt.
Ein interessantes Experiment zur virtuellen Spannung
Teilbild 8.3 erweitert Teilbild 8.2 mit einem Experiment. Zu diesem
Zweck ist das Potmeter P zwischen der virtuellen Spannung Uv und GND
geschaltet. Mit R2/R1 ergibt sich zwischen Ue und Ua eine Verstärkung
von -1. Wir wählen in diesem Experiment für R1 und R2, aber auch für P,
den selben Widerstandswert von je 10 k-Ohm. Wir geben auf Ue eine
Spannung von 1 VDC und am Ausgang Ua erscheint eine Spannung von -1 VDC,
weil R1 = R2 und Uv = 0 VDC. Ua verändert wegen P = 10 k-Ohm seinen Wert
von -1 VDC nicht. Warum auch, denn durch P fliesst schliesslich
praktisch kein Strom, weil Uv praktisch 0 VDC ist. Diese -1 VDC an Ua
bleiben aber auch, wenn wir an P drehen und den Wert z.B. auf 1 k-Ohm
oder weiter reduzieren. Warum denn auch nicht, denn wenn durch P kein
Strom fliesst, weil Ud praktisch 0 VDC ist, ändert sich auch nichts an
Ua. Also dann drehen wir den Wert von P weiter zurück und unterhalb
eines bestimmten Wertes, der weit unter 100 Ohm liegen kann, bemerken
wir, dass sich die DC-Spannung an Ua signifikant verändert. Wenn der
Wert von P drastisch reduziert wird, arbeitet der Opamp mit einer sehr
hohen Verstärkung, die durch die Gegenkopplung R2/P bestimmt wird. Die
Verstärkung zwischen Ue und Ua bleibt mit -1 stets aber trotzdem gleich
gross. Ist P sehr klein, wird die opamp-interne äquivalente
DC-Eingangs-Offsetspannung drastisch verstärkt. Unterhalb eines
kritischen Wertes von P gelangt Ua in die positive oder negative
Spannungsbegrenzung, die durch die Betriebsspannung bestimmt wird. Dies
ist ganz bestimmt der Fall, wenn Ud kurzgeschlossen ist. Bevor Ua jedoch
in die positive oder negative Spannungsbegrenzung getrieben wird,
beobachten wir noch etwas anderes, wenn wir beim Oszilloskopen genau
hinschauen. Wir bemerken, dass der DC-Spannung Ua auch noch eine
Rauschspannung überlagert ist. Dies kommt ebenfalls von der sehr hohen
Verstärkung durch R2/P, denn diese verstärkt die opamp-eigene
äquivalente Eingangsrauschspannung und die welche P selbst erzeugt.
Dieser "Nebenschauplatz" mit der DC-Offsetspannung lenkt aber vom
wirklichen Grund ab zu verstehen warum die Schaltung nicht funktionieren
kann, wenn der virtuelle GND mit dem echten GND kurzgeschlossen wird.
Der ganz einfache Grund ist schlichtweg der, dass Ud nicht ganz Null
sein kann, weil die Leerlaufstromverstärkung zwar sehr hoch, jedoch
endlich ist. Es ist aber diese extrem hohe Leerlaufverstärkung, welche
beinahe 0 VDC auf den invertierenden Eingang des Opamp regelt und so der
virtuelle GND von beinahe 0 VDC aufrecht erhält. Diese extrem niedrige
Spannung schliessen wir kurz, wenn der (Kurzschluss-)Widerstand sehr
niederohmig ist. Der Regelvorgang bricht dann ab, weil am invertierenden
Eingang auch die allerkleinste Spannung nicht variieren kann. Der Opamp
kann so seine verstärkende (regelnde) Aufgabe nicht mehr erfüllen.
An diesem Punkt der Diskussion könnte der "brilliante" Theoretiker
einwenden, dass der ideale Opamp mit einer unendlich hohen
Leerlaufverstärkung funktionieren müsste, wenn Ud kurzgeschlossen würde.
Kurzschliessen, würde hier aber nur gelten, wenn der
Kurzschlusswiderstand echt 0 Ohm hätte. Ein supraleitender Kupferdraht
bei wenigen Grad Kelvin, zum Beispiel. Tja, wenn aber Ud wegen der
unendlich hohen Leerlaufverstärkung echt 0 VDC beträgt, wie kann dann
durch den echten Null-Ohm-Widerstand ein Kurzschlussstrom fliessen, der
dazu fähig sein soll den Regelungsprozess, der den virtuellen GND mit
absolut 0 VDC erzeugt, zu unterdrücken? Also weniger als 0 VDC? Daraus
kann man schliessen, dass beim idealen Opamp der virtuelle und der echte
GND identisch sind und ein echter Kurzschluss zwischen den beiden
Opamp-Eingängen den Opamp in seiner verstärkenden Aufgabe nicht
behindert, weil dies dasselbe wäre, wie wenn man zwischen zwei echten
GNDs einen Kurzschluss herstellt...
Des langen Philosophierens kurzer Sinn: Für den Elektronikpraktiker
genügt es zu wissen, dass der virtuelle GND stets eine sehr kleine
Spannung hat und darum ist der virtuelle GND mit dem echten GND niemals
identisch. Um dies aber ein wenig besser zu verstehen, war der kurze
Ausflug in die Totalverwirrung schon sinnvoll, denn es gilt auch hier im
übertragenen Sinne der weise Spruch des Atomphysiker Niels Bohr
(1885-1962): "Wer über Quantenmechanik nachdenken kann, ohne wirr
zu werden im Kopf, hat sie nie wirklich verstanden." Und
verstehen wollen wir doch alle wie der Opamp funktioniert, oder?
Ein Ausflug in die urferne Vergangenheit: Jedermann weiss, dass
die Null in den Römischen Zahlen nicht existiert. Nun, es gibt Gelehrte
die entdekt haben sollen, dass in der vedischen Kultur im uralten Indien
diese Null bekannt war und man damit umgehen konnte. Dass die Null nach
dem Transfer über die schon damals bekannte "Seidenstrasse" in den
Vorderen Orient bald einmal verloren ging oder besser gesagt, vermutlich
verdrängt worden ist, hatte ihre Ursache wahrscheinlich darin, dass
diesen Völkern dort die Null und das Unendliche zu ominös waren. Sie
waren damit geistig überfordert. So jedenfalls lautet die Meinung derer,
die bei Ausgrabungen alter vedischen Kulturstätten in Sanskrittexten die
Zahl Null entdeckt haben. Wer weiss, vielleicht hat uns diese alte
Kultur noch heute mehr zu sagen, als die Zahl Null die sie uns vererbte,
aber das ist ein ganz anderes Thema. Ich beende hiermit das Thema über
die virtuelle Spannung von idealen und realen Opamps, über das
Unendliche und über die Null. Wir verlassen den kurzen "virtuellen"
Ausflug in die urferne Vergangenheit der vedischen Hochkultur und landen
gleich wieder in der harten Opamp-Alltagsrealität und befassen uns mit
dem Einschwingverhalten.
Das Einschwingverhalten
Dieses Thema wird bereits in Operationsverstärker I angedeutet. Es wird dort erklärt, dass es wegen solchem Einschwingverhalten und der damit involvierten Signalverzögerung nicht möglich ist, dass die Differenzspannung Ud schon in dieser Phase beinahe 0 VDC sein kann. Hier ist der Vorgang etwas ausführlicher beschrieben.
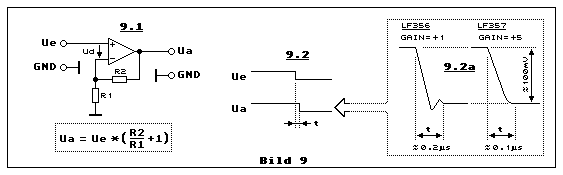
Bild 9 zeigt das skizzierte Einschwingverhalten bei einer kleinen
Ausgangsamplitude Ua (Output-Voltage-Swing) von etwa 100 mV beim LF356,
der eine minimale Verstärkung von +1 (0 dB), und beim LF357 (nicht mehr
erhältlich!), der eine minimale Verstärkung von +5 (14 dB) zulässt.
Diese beiden Minimalverstärkungen gelten auch für die beiden Diagramme
in Teilbild 9.2a, die jeweils zeitgedehnte Darstellungen von Ua aus dem
Teilbild 9.2 sind. Angeregt werden solche Einschwingvorgänge stets von
steilen Impulsflanken am Eingang Ue. Es gilt hier die nichtinvertierende
Verstärkerschaltung, wie sie in Teilbild 9.1 dargestellt ist.
Die zeitliche Verzögerung t von Ue nach Ua weicht in beiden Diagrammen
in Teilbild 9.2a nicht so sehr ab, wie man es vielleicht erwartet. Dies
kommt daher, dass beim LF357 die Unity-Gain-Bandbreite etwa gut 4 mal so
gross ist wie beim LF356, jedoch die Verstärkung +5 statt +1 beträgt.
Das heisst, in beiden Fällen ist die Grenzfrequenz und damit auch die
Impulsverzögerung t etwa ähnlich. Das Diagramm mit dem LF356 zeigt ein
schwaches Überschwingen (Overshooting), das unmissverständlich
daraufhinweist, dass die Schaltung mit der minimal zulässigen
Verstärkung von +1 leicht kritisch ist. Das Diagramm mit dem LF357
zeigt, dass dieser Opamp bei seiner minimal zulässigen Verstärkung von
+5 noch sehr stabil arbeitet, d.h. überhaupt keine Anzeichen von
Oszillation bei "Reizung" durch steile Impulsflanken zeigt.
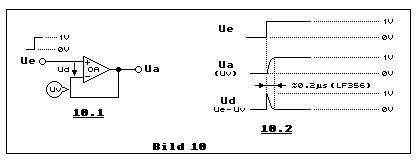
Bild 10 zeigt am Beispiel der nichtinvertierenden Verstärkerschaltung
mit Verstärkung 1 (Impedanzwandler), wie sich die differenzielle
Eingangsspannung Ud im Augenblick einer steilen Impulsflanke an Ue
bemerkbar macht. In Bild 9 kam die fallende und hier in Bild 10 kommt
die steigende Impulsflanke an Ue zur Geltung.
Es empfiehlt sich solches selbst mit einem Oszilloskopen zu testen.
Damit es mit einem einfachen nichtspeichernden Oszilloskopen möglich
ist, muss die Impulsfrequenz an Ue der Impulsverzögerung zwischen Ue und
Ua etwa angepasst sein. Beim Test eines LF356, sollte die Impulsfrequenz
(zeitsymmetrisches Rechtecksignal, Tastgrad ca. 0.5) mindestens
einige 100 kHz betragen. Ud kann man messen, in dem man an Kanal A
(Oszilloskop) das Signal von Ue und an Kanal B das Signal von Ua
anschliesst. Falls das Oszilloskop die Eigenschaft hat zwei
Eingangssignale zu subtrahieren, lässt sich auf dem Kanal A oder Kanal B
Ud messen, weil Ud die Subtraktion von Ue und Ua (Ua = Uv) ist. Es wird
hier mit einem Beispiel der Impulsamplitude von 1 V gearbeitet. Man kann
natürlich auch mit andern Werten experimentieren und so durch
Beobachtung am Bildschirm erfahren, ab welcher Impulsamplitude nicht
mehr die Unity-Gain-Bandbreite sondern die Slewrate als
Geschwindigkeitsbegrenzer agiert. Viel Spass beim lebendigen
Experimentieren!
Links
(1) Operationsverstärker I:
Virtuelle Masse, Slewrate, Unity-gain,
Gegenkopplung, Arbeitspunkt.
(2) Operationsverstärker II:
Gain, DC-Offset, kapazitive Belastung, Einschwingverhalten
und Stabilität.
(3) Vom Operationsverstärker zum
Schmitt-Trigger
(4) Gegentakt-Endstufe:
Theorie und Grundlage...