Netzteil-Testgerät I
Inhaltsverzeichnis
-
1. Einleitung
2. Statisches und dynamisches Messen
3. Stromquelle - Stromsenke
4. Einfache Stromsenke mit Opamp und Transistor
5. Stromsenke mit Opamp und Darlington
6. Das Netzgerät/teil-Testgerät
7. Technische Daten zu Bild 6
8. Linkliste
1. Einleitung
Etwa anfangs der 1980er-Jahren und weiter zurück war es auf Grund des
meist unbefriedigenden Angebotes im Elektronikmarkt noch sehr
selbstverständlich, dass man Netzteile und Netzgeräte selbst baute.
Heute ist der Markt überflutet mit diversesten Netzgeräten und
(Schalt-)Netzteilen und doch kommt es immer wieder vor, dass man selbst
etwas entwickeln muss, wie z.B. in der Medizinalelektronik oder für
andere Sonderanfertigungen. Für solche Netzgeräte und Netzteile, aber
auch für gekaufte "ab der Stange", ist es oft sinnvoll und zweckmässig
diese genau zu prüfen.
Das vorliegende Testgerät baute ich etwa Ende der 1970er-Jahre und es
ist bis heute immer wieder im Einsatz und leistet seinen hervorragenden
Dienst. Es besteht aus zwei elektronisch steuerbaren
Konstant-Stromsenken, welche symmetrisch einen postiv und negativ gleich
grossen Strom ziehen, sofern Spannungsquellen angeschlossen sind. Man
kann also Netzgeräte und Netzteileile mit einfacher oder symmetrischen
Ausgangsspannungen testen. Diese Spannungen dürfen variabel einstellbar
oder fest eingestellt sein. Der eingestellte Stromwert der Stromsenken
bleibt, unabhängig vor den zu prüfenden Spannungen konstant.
Mit einer rechteckförmigen Steuerspannung kann man zwischen zwei
einstellbaren Stromwerten umschalten. Dies ermöglicht das dynamische
Verhalten der Ausgangsspannungen des Netzgerätes oder Netzteiles mittels
Oszilloskop genau zu beobachten, um damit das Mass der Stabilität zu
beurteilen.
Dieser Elektronik-Minikurs dient - wie alle andern auch - zur Hauptsache
nicht nur dazu den Inhalt 1:1 umzusetzen, er soll Anreiz dafür sein
eigene Ideen zu entwickeln, jedoch nützliche Teile oder Ideen von diesem
Elektronik-Minikurs miteinzubeziehen. Dies gilt hier besonders dann,
wenn man ein Testgerät mit ganz anderen Strombereichen und vielleicht
auch ganz andern Spannungen realisieren muss. Die Verlustleitungen an
den Transistoren haben ganz andere Werte. Der Leser muss die Schaltung
seinen Bedürfnissen anpassen. Wobei er sich in der Berechnung von
Transistorschaltungen auskennen muss. Vielleicht eignen sich besser
Power-MOSFETs anstelle von bipolaren Leistungstransistoren, denn diese
haben bekanntlich den wichtigen Vorteil, dass sie den sogenannten
zweiten Durchbruch nicht haben. Ebenso wichtig ist das Dimensionieren
von Kühlprofilen und vieles andere mehr.
2. Statisches und dynamisches Messen
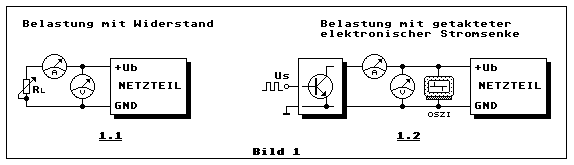
Teilbild 1.1 zeigt im Blockschaltbild die einfachste Methode eine
Spannungsquelle zu testen. Anstelle eines Netzgerätes/teiles kann es
auch eine Batterie oder ein Akku sein. Man misst am Ausgang der
Spannungsquelle die Spannung, z.B. mit einem Multimeter, symbolisch
dargestellt mit dem Messinstrument V. Die Netzspannung wird mit einem
einstellbaren Lastwiderstand RL belastet, wobei im
Stromkreis ein Messinstrument zur Messung des Stromes (Bezeichnung A für
Amperemeter) eingeschlauft ist. Bei kleinen Strömen und Leistungen
eignen sich als einstellbare Lastwiderstände gerade noch Potentiometer
(Potmeter) im Watt-Bereich, für grosse Ströme kommen grosse
Schiebewiderstände zum Einsatz. Mit dieser einfachen Methode kann man
allerdings nur gerade das statische Verhalten der Spannungsquelle unter
Strombelastung messen, bzw. mit einem Oszilloskopen beobachten. Ein
weiterer Nachteil ist, wenn die Spannung am Ausgang der Spannungsquelle
varriert, ändert sich auch der Strom. Will man bei einer
Spannungsänderung testweise den selben Strom messen, muss der
Lastwiderstand von Hand nachgesteuert werden.
Dieses Problem nimmt einem die elektronische Konstant-Stromsenke ab. Sie
hat die selbe elektronische Eigenschaft wie die Konstant-Stromquelle.
Der differenzielle Innenwiderstand ist theoretisch unendlich gross, weil
sich der Strom auf Grund einer Spannungsänderung praktisch nicht ändert.
In der Praxis trifft dies aber nicht zu, jedoch kann der differenzielle
Innenwiderstand, je nach Qualität der Konstant-Stromsenke bzw.
Konstant-Stromquelle, sehr hochohmig sein. Ein Beispiel: Eine
Stromsenke/quelle erhält eine Spannungsänderung von 10 V und dabei
ändert sich der Strom von 1.000 A zu 1.001 A. Gemäss ohmschem Gesetz
resuliert ein differenzieller Widerstand von 10 k-Ohm während der
statische Innenwiderstand nur 10 Ohm (bei 10 V) beträgt. Bei einer
Konstant-Spannungsquelle verhält sich die Situation genau umgekehrt,
weil eine grosse Stromänderung kaum eine Spannungsänderung verursacht.
Teilbild 1.2 zeigt das Blockschaltbild einer elektronischen Stromsenke,
dessen Strom mit einer Schaltspannung Us (s = schalt) zwischen zwei
Werten mittels eines Taktgenerators umgeschaltet werden kann. Damit ist
es möglich mittels eines Oszilloskopen die dynamischen Schalt- bzw.
Einschwingvorgänge der Ausgangsspannung zu beobachten und beurteilen.
Wir betrachten dazu Bild 2:
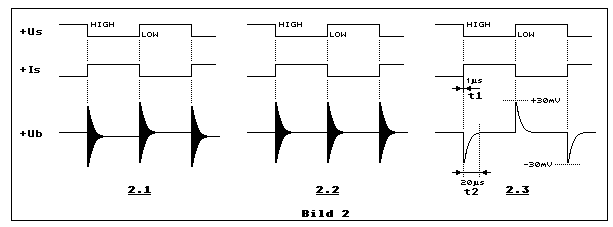
Diese Diagramme in Bild 2 beziehen sich bereits auf das vollständige
Schaltschema in Bild 6. Um diese Diagramme zu verstehen, muss man die
Schaltung von Bild 6 jetzt noch nicht miteinbeziehen. Man muss hier nur
verstehen, dass mit elektronischen Mitteln der Strom, der vom Netzteil in
die Stromsenke fliesst (siehe Teilbild 1.2), sehr schnell zwischen zwei
Werten umgeschaltet werden kann. Diese Geschwindigkeit nennt man auch
Flankensteilheit, den man beim Strom z.B. in A/µs oder A/ms angibt.
Was zeigen uns die drei Diagramme in Bild 2? Die Steuerspannung +Us (s =
steuer), ein Logiksignal, schaltet den Strom Is (s = Senke) zwischen
zwei Werten und die Ausgangsspannung +Ub reagiert auf drei Arten, die
wir in den drei Teilbildern genauer betrachten:
1.
Man erkennt in der dynamischen Wiedergabe von +Ub des Netzteiles eine
hochfrequente Instabilität, die durch die Stromumschaltung angeregt
wird. Diese hochfrequenten Schwingungen sind durch die schwarzen Flächen
angedeutet und sie zeigen eine kritische Dämpfung. Mit einer steilen
Stromflanke wird die hochfrequente Schwingung angeregt und klingt, ganz
ähnlich wie bei einem Glockenschlag, anschliessend wieder ab. Mann nennt
dies eine aperiodische Dämpfung. Im Gegensatz dazu, wird eine
periodische Schwingung nicht gedämpft, die Schwingungen setzen sich
fort. Die Teilbilder 2.1 und 2.2 zeigen, dass die Spannungsquelle an der
Stabilitätsgrenze arbeitet. Sie neigt mit diesem Verhalten zum
hochfrequenten Oszillieren. Die Systemdämpfung der
Spannungsregelschaltung ist einfach gerade noch gross genug, dass die
Oszillation nicht durch Selbsterregung einsetzt und dauerhaft vorliegt.
Aber diese doch relativ schwach gedämpfte Schwingung zeigt uns, dass es
empfehlenswert ist diesem Netzgerät/teil diese Instabilität
abzugewöhnen. Wie man dies tut, kommt ganz auf die Schaltung des
Netzgerätes/teiles an und ist nicht Gegenstand dieses
Elektronik-Minikurses. Es gibt allerdings eine kleine Einführung zu
diesem Thema in (3) im Unterkapitel Die
zusätzliche Frequenzgangkompensation mit C3 und R5.
2.
Wir kommen jetzt zur statischen Betrachtung. Zwischen den
Stromumschaltmomenten erkennen wir gerade Spannungslinien (+Ub).
Allerdings ist die Spannung +Ub beim höheren Strom konstant etwas
niedriger als beim niedrigeren Strom, wie dies Teilbild 2.1 zeigt. Dies
kann grundsätzlich zwei Ursachen haben: Entweder arbeitet die
Spannungsregelung unbefriedigend oder die Verlustwiderstände zu den
Anschlüssen beim Netzgerät/teil oder beim Verbraucher (falls man dort
messen will) sind zu gross. Abhilfe bieten hier Netzgeräte/teile mit
Spannungssensoranschlüssen, mit denen es möglich ist, vom Verbraucher
die Spannung zur Regelschaltung zurückzuführen. Diese rückgeführte
Spannung wird dann regeltechnisch verarbeitet. Dieser regeltechnische
Trick erlaubt aber meist keine Übertreibungen. Dies soll heissen, man
darf sich nicht zu dünne und/oder zu lange verlustreiche Leitungen
erlauben und dann mittels Sensorschaltung darauf hoffen, dass die
Spannungsregelschaltung diese Fahrlässigkeit automatisch und sauber
korrigiert. Wenn man damit übertreibt, reizt man die Regelschaltung oft
in Richtung mehr dynamischer Instabilität!
Es stellt sich hier die Frage, was eine gute statische Stabiltät ist.
Dies kann generell nicht beantwortet werden, weil es ganz von der
Anwendung abhängt. An ein Labornetzgerät werden beispielsweise besonders
hohe Anforderungen gestellt, für den Einsatz in einem industriellen
Gerät - allerdings auch je nach Anwendung - eher geringere. Wir kommen
zu einem praktischen Beispiel eines Labornetzgerätes mit sehr guten
Stabilitätseigenschaften, wie sie in Teilbild 2.3 zum Ausdruck kommen.
Der Elektronik-Minikurs in (1) präsentiert ein
renoviertes altes Netzgerät. Ich erreichte mit dieser Renovation u.a.
einen statischen Innenwiderstand von 1 Milli-Ohm! Dies bedeutet, dass
eine Stromänderung von 1 A eine Spannungsänderung von 1 mV bewirkt. Dies
erreichte ich mit dicken Leitungen von der Regelschaltung zu den
Anschlussbuchsen und mittels bereits angedeutetem Spannungsfeedback von
diesen Buchsen zur Regelschaltung. Die Rausch/Stör-Spannung unter Last
ist wesentlich geringer, weil man sonst diese 1 mV gar nicht messen
könnte. Teilbild 2.2 zeigt eine Ausgangsspannung mit guter statischer
Spannungsstabilität. Die hochfrequente Instabilität, entsprechend
Teilbild 2.1, ist hier noch nicht beseitigt.
3.
Teilbild 2.3 zeigt das Diagramm einer statisch und dynamisch stabilen
Spannungsregelung. Wenn die Zeit der Stromänderung t1 (Flankensteilheit)
viel kleiner ist als Regelgeschwindigkeit t2 der
Spannungsregelschaltung, ereignet sich bei jeder Stromumschaltung ein
Spannungsüber- oder Spannungsunterschwingen. Wird plötzlich mehr Strom
hinzugeschaltet, gibt es eine kurzzeitige Unterspannung. Wird plötzlich
der Strom reduziert, gibt es eine kurzzeitige Überspannung. Das lässt
sich gar nicht verhindern, weil die Regelschaltung das Ereignis immer
erst erfährt, wenn es eingetreten ist. Was man tun kann, ist eine
schnelle Regelschaltung realisieren, so dass t2 so klein wie möglich
ist. Die Amplituden dieses Über- und Unterschwingens kann allerdings mit
einer kapazitiven Belastung der Ausgangsspannung des Netzteiles mit
einem Kondensator genügend hoher Kapazität drastisch reduziert werden.
Ein guter Wert für diese Einschwingzeit liegt im unteren 10-µs-Bereich
und der Wert des maximalen Amlitudenwertes im unteren 10-mV-Bereich.
Diese Zahlenwerte stammmen aus dem bereits genannten Elektronik-Minikurs
(1).
3. Stromquelle - Stromsenke
Stromquelle oder Stromsenke, das ist hier die Frage? Nun ja, allerdings nur eine formale und keine schaltungstechnische, denn da gibt es keinen Unterschied. Ob es eine Stromquelle oder Stromsenke ist, ist reine Definitionssache in Funktion der Schaltungsumgebung. Etwas Aufklärung dazu liefert Bild 3:
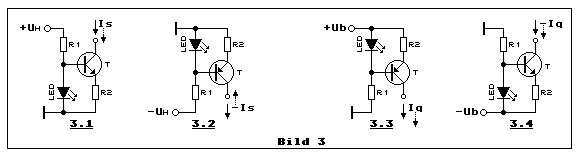
Teilbild 3.1 zeigt uns eine Stromsenke mit dem Stromanschluss Is. Von
einer externen Spannungsquelle fliesst über Is ein konstanter Strom über
T und R2 nach GND. Der Stromlieferant ist also eine externe
Spannungsquelle, deshalb ist die so gezeichnete Schaltung eine
Stromsenke. Man könnte es auch so betrachten: Wenn anstelle der
Elektronik zwischen dem Anschluss Is und GND nur ein Widerstand
geschaltet wäre, wäre dieser Widerstand die Stromsenke, allerdings wäre
der Strom Is nicht spannungsunabhängig konstant.
Die Stromquellen- bzw. Stromsenkenschaltungen die hier gezeigt werden,
studiert man im folgenden Elektronik-Minikurs
(5).
Teilbild 3.2 zeigt ebenfalls, rein formal, eine Stromsenke, jedoch eine
mit negativem Stromfluss. Der Strom fliesst von einer externen negativen
Spannungsquelle über den Anschluss -Is, T und R2 nach GND. Der Pfeil
oberhalb der Bezeichnung -Is zeigt dies, aber die "offizielle"
Stromrichtung zeigt (natürlich) stets von Plus (hier GND) nach Minus,
wie dies der Pfeil links von -Is darstellt. In Teilbild 3.1 zeigen beide
Pfeile in die selbe Richtung.
Teilbilder 3.3 und 3.4 sind Stromquellen. +Ub bzw. -Ub sind die
Spannungseingänge, auf diese folgt je die Konstant-Stromquelle und an
dessen Ausgängen fliesst der Strom in Richtung weniger postiver bzw.
weniger negativer Spannung. Dies kann in beiden Fällen GND sein, jedoch
ebenso -Ub (Teilbild 3.3) bzw. +Ub (Teilbild 3.4).
Damit wäre die Sache mit Stromquelle und Stromsenke ein wenig
aufgeklärt. In allen vier Teilbildern ist es das selbe
Schaltungsprinzip. Man kann der Auffassung sein, dass diese
Unterscheidung von Quelle und Senke übertrieben ist und man betrachtet
es vom Standpunkt der Schaltung immer als Stromquelle. Allerdings fällt
es mir doch etwas schwer, eine elektronisch geregelte Last, die ein
Netzgerät/teil testet, als Stromquelle und nicht als Stromsenke zu
bezeichnen. Darum hier dieser Aufwand. Ich hoffe aber trotzdem, die
Verwirrung ist nicht so total wie sich einmal der berühmte Physiker
Niels Bohr (1885-1962) über die Quantenmechanik äusserte: "Wer
über Quantenmechanik nachdenken kann, ohne wirr zu werden im Kopf, hat
sie nie wirklich verstanden." Wobei es einen signifikanten
Unterschied zwischen Bohr und mir gibt: Wenn hier eine Verwirrung
zustande kommt, dann deshalb, weil ich diese soeben angerichtet habe und
nicht die Physik selbst die Ursache ist... :-)
4. Einfache Stromsenke mit Opamp und Transistor
Bei den Stromsenken und Stromquellen wie sie in Bild 3 gezeigt
werden, ist stets die Referenzspannungsqsquelle im Basiskreis und der
Widerstand im Emitterkreis strombestimmend. Eine LED als
Referenzspannungsqsquelle hat den grossen Vorteil, dass ihr
Temperaturkoeffizient praktisch gleich gross ist wie die
Basis-Emitter-Schwellenspannung des Transistors mit etwa -2 mV/°C.
Wird die LED von aussen gleich stark erwärmt wie der
Transistor, kompensieren sich die beiden Temperaturkoeffizienten und man
erhält mit wenig Aufwand eine sehr temperaturstabile
Konstantstromquelle/senke. Wenn sich jedoch der Transistor, wegen zu
hoher Verlustleistung, mehr erwärmt als die LED, verschlechtert sich
die Kompensationseigenschaft schnell. Mehr dazu erfährt man in
(5).
Diesem Problem kann man ausweichen, wenn ein Operationsverstärker mit
einbezogen wird, in dem dieser mit seiner Regeleigenschaft sehr viel für
einen konstanten Strom beiträgt. Die Stabilität des Stromes ist zur
Hauptsache nur von einer stabilen Spannung am nichtinvertierenden
Eingang und einem Lastwiderstand im Emitterkreis eines Transistors
abhängig. Realisiert man diese stabile Spannung mittels Potmeter
variabel, hat man hier eine einstellbare Konstantstromsenke, - die man
ja nach "Blickwinkel" natürlich auch als Konstantstromquelle betrachten
kann. Wir kommen damit zu Bild 4:
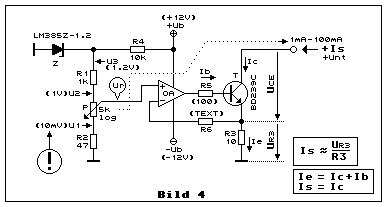
An +Is wird der Strom aus einer externen Spannungsquelle +Unt (nt =
netzteil) gemessen. Die Schaltung dient hier als Stromsenke. Für eine
sehr stabile Referenzspannung empfiehlt sich eine sogenannte
Bandgap-Referenzspannungsquelle Z, wie sie genauer im
Elektronik-Minikurs (6) beschrieben ist.
Wir analysieren diese Stromsenkeschaltung und hinterfragen sie kritisch.
Es beginnt mit der Referenz-Spannungsquelle Z, dem bekannten zweipoligen
Bauteil LM385Z-1.2, mit einer ultrastabilen Spannung von 1.2 VDC. Man
ist geneigt dieses Bauteil Diode oder Bandgap-Diode zu nennen. Zu
unrecht, weil in ihr steckt eine doch recht komplexe integrierte
Schaltung (IC) mit immerhin 14 Transistoren. Der Betriebsstrom, bei dem
die stabile Spannung garantiert wird, reicht von 20 µA bis 20 mA, was
einem Faktor von 1000 entspricht. Keine Zenerdiode der Welt könnte einer
solchen integrierten Superschaltung Paroli bieten!
Potmeter P liefert im Bereich von 10 mVDC bis 1VDC die variable aber
hochstabile Eingangsspannung an den nichtinvertierenden Eingang des
Opamp OA. Der Ausgang des OA steuert über R5 die Basis des Transistors T
und vom Emitter aus erfolgt die volle Gegenkopplung (Verstärkung = 1)
zum invertierenden Eingang des OA. Da es im eingeschwungenen Zustand der
gesamten Schaltung idealerweise am nichtinvertierenden und
invertierenden Eingang des OA stets die selbe Spannung hat, oder anders
gesagt, die Differenspannung dieser beiden Eingänge 0 V ist, liegt
logischerweise die selbe Spannung Ur über R3. R3 ist am Zustandekommen
des Emitterstromes Ie verantwortlich, der sich aus dem Quotienten des
Spannunungsabfalles über R3 und aus dessen Widerstand ergibt. Im
vorliegenden Beispiel beträgt der Strom, wenn das Potmeter die maximale
Spannung von 1 VDC erzeugt, 100 mA. Mit P kann man einen Strom Ie
zwischen 1 mA und 100 mA einstellen.
Damit sind wir an dem Punkt angelangt, wo wir die Schaltung kritisch
unter die Lupe nehmen. Wir verwenden mit Z eine hochstabile
Referenzspannung. Garantiert dies aber auch, dass wir eine ebenso hohe
Stromstabilität von Ie und Is erzielen? Keineswegs! Wenn man
herunterfahren will bis 1 mA, müssen wir schon einen Opamp mit sehr
niedriger DC-Offset-Spannung verwenden, damit die 10 mVDC am
nichtinvertierenden Eingang auch wirklich einen Emitterstrom Ie von
exakt 1 mA erzeugt. Wenn das allerdings nicht so wichtig ist und einem
nur Ie, bzw. Is interessiert, den man mit P einstellen will, muss die
minimale Spannung U1 einfach niedriger gewählt werden, damit eine
allfällig postive DC-Offsetspannung sicher kompensiert werden kann. Man
kann R2 auch weglassen und dieses Ende von P direkt mit GND verbinden.
Nicht ganz so kritisch ist - auch bei den älteren Opamps - der
temperaturabhängige DC-Offsetspannungsdrift. Beim Oldy-Opamp "741" sind
es 15 µV/K. Trotzdem bedeutet dies, dass bei einer Temperaturänderung
von 20 K, der Emittertrom Ie sich von z.B. exakt 1.00 mA auf 1.03 mA
oder auf 0.997 mA verändern kann. Für viele Anwendungen ist diese
geringe Unpräzision irrelevant. Bei der Verwendung eines Opamp mit
bipolaren Eingangsstufen gilt diesbezüglich noch die Regel, dass der
Quellwiderstand an beiden Eingängen möglichst gleich sein soll, was
durch die Variation von P aber gar nicht möglich ist. Deshalb kann man
auf R6 gleich verzichten oder man definiert ihn auf einen ungefähren
Mittelwert, hier etwa 1 k-Ohm. Benutzt man einen Opamp mit JFET- oder
MOSFET-Eingangsstufen, erübrigt sich diese Überlegung, weil die
Eingangswiderstände nicht nur extrem hochohmig sind in Relation zu den
Widerstandswerten der angeschlossen Netzwerke, selbst dann wenn diese im
M-Ohm-Bereich liegen, die sogenannten Eingangs-Offset- und
Eingangs-Biasströme sind auch extrem niedrig.
Jetzt kommen wir zur Sache mit dem Kollektorstrom Ic. Ist dieser
eigentlich gleich gross wie der Emitterstrom Ie oder nicht? Er ist es
nicht. Ic ist um den Betrag des Basisstromes Ib niedriges als Ie. Nun,
wenn die Stromverstärkung gross ist, z.B. um 100 oder sogar mehr, ist
das meist unkritisch, wenn sehr hohe Präzision und Konstanz nicht so
wichtig sind. Sind aber hohe Ströme im A-Bereich und geringe
Kollektor-Emitter-Spannungen im Spiel, kann die Stromverstärkung sehr
niedrig werden und der Anteil des Basisstromes nimmt zu. Dies lässt sich
leicht überprüfen in dem man die Spannung über R5 misst. Alleine
deswegen empfiehlt sich im Basiskreis ein Widerstand. Durch die Messung
der Spannung über R5 kann man sehr gut die Stromverstärkung von T in
Abhängigkeit von UCE überprüfen. Wenn der Wert von
100 Ohm für R5 eine höhere Spannung als einige VDC erzeugt, empfiehlt
sich einen niedrigeren Wert zu wählen. Dazu müsste der Basisstrom
allerdings mehr als 10 mA betragen und das erreicht er nur, wenn
UCE so niedrig ist, dass T in Sättigung liegt (Ic =
100 mA). Dies ist dann der Fall wenn +Unt, die sich aus
UCE plus UR3 zusammensetzt,
sehr niedrig ist. Es ist dabei auch noch zu bedenken, dass OA den Strom
von 10 mA liefern muss. Kann er das nicht, bricht die Stromregelung
zusammen. Ein "741" schafft dies kaum, ein anderer nicht ganz so alter
Oldy, der LF351, ein JFET-Opamp, schon eher.
Funktionell wird R5 nicht benötigt. Der Widerstandswert in Klammer
drückt aus, dass man ihn überbrücken oder ändern kann. Er sollte auch
noch aus einem andern Grund nicht zu hoch gewählt werden: R5 und die
Kollektor-Basis-Kapazität von T erzeugen ein Tiefpassfilter
(Millereffekt). Wenn dessen Grenzfrequenz zu niedrig ist, wird die
Regelgeschwindigkeit des Regelsystems reduziert. Dem kann man allerdings
entgegenwirken, in dem pararallel zu R5 ein Kondensator geschaltet wird,
wie dies Bild 6 illustriert (dort ist es R9 und R10).
Man sollte bei einem Schaltungsentwurf auf jedenfall erst einen sauberen
Testaufbau realisieren und die Stabilität der Schaltung testen bevor man
eine Leterplatte entwirft! Damit erspart man sich manchen Ärger! Sauber
bedeutet, dass man ein wilder Drahtverhau auch beim Testaufbau
vermeidet. Ein sauberer Versuchsaufbau trägt wesentlich zum stabilen
Funktionieren einer analogen Schaltung bei!
Anstelle dieses bipolaren Transistors könnte man auch einen
Leistungs-MOSFET einsetzen, dann gibt es das soeben beschriebene Problem
der unteschiedlichen Ströme im Hauptstrompfad nicht, weil kein Gatestrom
fliesst. Der Drainstrom wäre identisch mit dem Sourcestrom. Es gibt aber
mit der oft recht grossen Gate-Source-Kapazität von "starken"
Leistungs-MOSFETs ein nicht zu unterschätzendes Stabilitätsrisiko, das
mit einem Versuchsaufbau zuerst genau abgeklärt werden muss! Leider habe
ich mich mit Leistungs-MOSFETs im linearen Betrieb zuwenig befasst, um
einen Elektronik-Minikurs zum Thema Stromquelle/senke zu schreiben.
Vielleicht ändert sich dies irgendwann...
Ein paar Worte zur Betriebsspannung ±Ub. Es sind ±12 VDC angegeben. Das
ist nur ein Beispiel. Diese Betriebsspannung ist keineswegs zwingend.
+Ub muss nur so gross sein, damit Z sicher betrieben werden kann und die
für die Regelung benötigte Ausgangsspannung des OA sicherstellt. Ohne
Verwendung von R5 beträgt diese Spannung UR3 +
UBE(T) und das sind im vorliegenden Beispiel etwa
1.8 VDC. Es kommt auf den Typ des Opamp an, wieviel positive
Betriebsspannung er selbst benötigt um diese Ausgangsspannung sicher zu
liefern. Für viele moderne Opamps genügen auf jedenfall +5 VDC.
Verwendet man einen Opamp mit ein- und ausgangsseitiger
Rail-to-Rail-Eigenschaft, braucht man auch keine negative
Betriebsspannung -Ub. Es genügen +Ub und GND. Da aber dieser
Elektronik-Minikurs auf eine symmetrische Stromtestschaltung (Bild 6)
hinausläuft, sind auch diese Schaltungen davor mit symmetrischen
Betriebsspannungen gezeichnet und beschrieben.
5. Stromsenke mit Opamp und Darlington
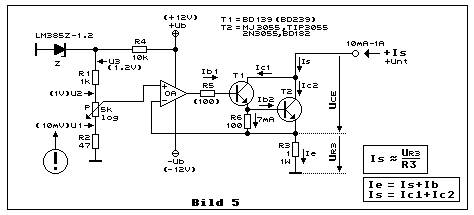
Der Unterschied zwischen Bild 5 und Bild 4 ist minimal und trotzdem
bietet die Schaltung in Bild 5 einen wesentlichen Vorteil. Es ist die
NPN-Darlingtonschaltung
(4)
die hier aus zwei Einzeltransistoren besteht. Man kann aber ebenso einen
intergrierten Darlington verwenden. Mit einem Darlington erreicht man
eine Stromverstärkung bis zu mehreren 10'000 und somit ist Ib1 sehr
niedrig und belastet den Ausgang des OA kaum noch. Ib1 fällt, betreffs
Unterschied von Is und Ie, praktisch nicht mehr ins Gewicht. Wenn die
Basis-Emitter-Schwellenspannung von T2 erreicht ist, leitet T2. Is teilt
sich auf in den grossen Anteil Ic2 und in den kleinen Anteil Ic1. Ib2
bildet sich aus Ic1 und Ib1. Ie entsteht zur Hauptsache aus Ic2 und Ic1.
Hinzu kommt Ib1 und sein sehr gringer Anteil liegt in der Regel weit
unterhalb eines Promilles des Gesamtstromes Is oder Ie. Man kann sagen,
Is entspricht praktisch Ie.
Im soeben beschriebenen Zustand fliesst über R6 ein Strom von etwa 7 mA.
Dies bedeutet, wenn Is geringer ist als diese 7 mA, arbeitet nur T1. Mit
dieser Massnahme reduziert sich die Stromempfindlichkeit der
Darlingtonstufe bei besonders niedrigen Mesströmen Is. R6 und der Strom
durch ihn ist willkürlich gewählt und unkritisch. R6 sollte einfach
nicht so niederohmig gewählt werden, dass T1 einen zu grossen Strom
liefert und deswegen bei relativ hoher Spannung +Unt zu heiss werden
könnte. Bei 7 mA und z.B. 30 VDC sind das bloss 210 mW. T1 muss also
nicht speziell gekühlt werden, wenn nur er alleine aktiv wäre. Bei einem
Strom Is von maximal 1 A fliesst allerdings ein T2-Basisstrom Ib2 von
gut 10 mA. Die Stromverstärkung des alten NPN-Arbeitspferdes MJ3055,
TIP3055 (Gehäuse TO218) oder 2N3055 (Gehäuse TO3) beträgt maximal 100
bei einer Basis-Emitter-Spannung von minimal 2 VDC und einer
Chiptemperatur von 25 °C und mehr.
Der Strom von 7 mA steigt auf minimal 17 mA. Legen wir noch einen dazu
und sagen 20 mA. Damit steigt die Verlustleistung von T1 auf 600 mW bei
einer Spannung +Unt von 30 VDC. Es empfiehlt sich für T1 eine kleine
Kühlfahne. Dass T2 ausreichend gekühlt werden muss, ist klar, da T2 bei
30 VDC und 1 A immerhin eine Leistung von 30 W verheizt. Die maximale
Kollektor-Emitter-Spannung darf beim 2N3055 (und die oben erwählten
3055-Alternativen) und einem Kollektorstrom von 1 A mehr als 50 VDC
betragen, sofern T2 ausreichend gekühlt wird. Wenn man eine so hohe
Spannung anlegt, muss man aber auch daran denken für T1 ein Typ
einzusetzen, der diese Spannung erträgt. Gibt man sich z.B. mit +Ub = 20
VDC zufrieden, erlaubt der 2N3055 ein Strom bis maximal 6 A (das ist
allerdings alleroberster Limit!) bei ebenfalls sehr grosszügig
ausgelegter Kühlung. Das Diagramm im Datenblatt des 2N3055 betreffs
Stromverstärkung zeigt jedoch, dass dieser Wert sich auf etwas mehr als
20 reduziert. Dies bedeutet, dass T1 viel mehr zu leisten hat, weil
dieser muss in die Basis von T2 einen Strom 300 mA liefern. T1
verbraucht bei rund 20 VDC somit eine Leistung von 6 W und das bedeutet
ganz eindeutig, dass T1 massiv gekühlt werden muss. Ein BD139 eignet
sich nicht mehr. Es muss mindestens ein BD239 her!
Aus all diesen Überlegungen kann man lernen, dass man entweder nach
einem modernen Leistungstransistor suchen muss, der bei diesem
Kollektorstrom eine wesentlich höhere Stromverstärkung hat oder man
benutzt gleich einen integrierten Darlington mit genügend hoher
Gesamtstromverstärkung. Oder ein anderer Weg besteht darin, dass man
eine Stromsenkeschaltung mit einem Power-MOSFET dimensioniert. Wie
auch immer, zu solchen Änderungen ist das Studium der Datenblätter und
die präzisen Kenntnisse über die Komponenten, die man einsetzt,
erste Voraussetzung und dann kommt die Praxis...
Zur Berechnung von Kühlkörpern findet man etwas im Elektronik-Minikurs
(3). Berechnungsgrundlagen bekommt man auch von
den Herstellern von Kühkörpern und Kühlprofilen. Dazu kommt, dass man
sich mit dem sogenannten Safety-Operating-Area (SOA) und dem sogenannten
Second-Breakdown von bipolaren Leistungstransistoren beschäftigen muss,
falls dieser Transistortyp zum Einsatz kommen sollten.
6. Das Netzgerät/teil-Testgerät
Wie bereits erwähnt, das folgende Testgerät in Bild 6 baute ich vor mehr als 25 Jahren und benutze es auch heute immer wieder. Ich habe es für diesen Elektronik-Minikurs bloss geringfügig verbessert. Bild 6 enthält zwei umschaltbare symmetrische Stromtestbereiche ±Is und die mit einem externen Rechtecksignal Us steuerbare Umschaltung zwischen zwei Stromwerten von ±Is ist mit einer Konstantstromquelle ausgestattet, welche die Einstellbarkeit verbessert.
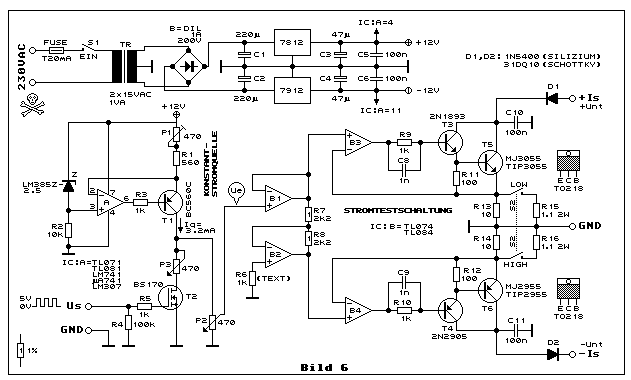
Die Schaltung in Bild 5 ist grundsätzlich identisch mit dem Teil der
Schaltung in Bild 6, der aus dem Opamp IC:B3 und den Transistoren T3 und
T5 besteht. Hat man den Text zu Bild 5 verstanden, ist klar, wie dieser
Schaltungsteil in Bild 6 funktioniert. Ebenso klar ist es aber auch, wie
der Schaltungsteil in Bild 6 mit IC:B4 und den Transistoren T4 und T6
funktioniert. Der einzige Unterschied ist der, dass hier das selbe im
negativen Strombereich passiert. Das Testgerät eignet sich für den Test
von Netzgeräten/teilen mit symmetrischen, aber auch asymmetrischen
Ausgangsspannungen. Für die Stromsenken spielt es keine Rolle, ob ein
Netzteil mit ±12 VDC oder z.B. eines mit +12 VDC und -9 VDC getestet
wird. In beiden Beispielen fliessen in +Is und in -Is die selben Ströme.
Will man unterschiedliche Ströme, kann man dies leicht mit einer
Änderung der Verstärkung des IC:B2 (R7, R8) erreichen. Dabei bleiben die
Stromverhältnisse, unabhängig von Ue, stets gleich.
Mit dem zweipoligen Schalter S2 ist der Strombereich von ±Is in zwei
Stufen umschaltbar. In Stellung LOW kann ein Strom bis maximal 150 mA,
in Stellung HIGH bis maximal 1.5 A gemessen werden. Verwendet man für
die zwei Potmeter P2 und P3 solche mit 10 oder 20 Gängen, ist die
Einstellung im unteren Strombereich besonders leicht. Alternativ dazu
und billiger sind einfache Potmeter mit logarithmischer
Widerstandskurve. Auch damit ist der untere Bereich, genau so wie bei
der Lautstärke eines Audiogerätes, leichter einstellbar.
Die beiden Dioden D1 und D2 dienen als Verpolungsschutz. Wenn ohne diese
Dioden das Testgerät betrieben wird, die Anschlüsse am zu testenden
Netzteil verpolt angeschlossen werden und die Spannung ±Unt grösser ist
als die maximale inverse Basis-Emitter-Schwellenspannung (T3/T5 und
T4/T6) von meist etwa 5 V, kann einiges zerstört werden, - auch der
Quad-Opamp IC:B. Sind D1 und D2 Silziumdioden, erhöht sich die minimale
Spannung ±Unt, je nach Stromstärke, um einen Betrag von ±0.7 bis etwa ±1
VDC. Allerdings lässt sich diese Spannung auf mindestens die Hälfte
reduzieren, wenn Schottky-Leistungsdioden zum Einsatz kommen.
Für die beiden Regelschaltungen wird mit IC:B3 und IC:B4 je ein Opamp
benötigt. Da noch zwei weitere Opamps, IC:B1 und IC:B2, für die gesamte
Stromtestschaltung benötigt werden, lohnt sich der Einsatz eines
Quad-Opamp. Es eignet sich der altbekannte und tradionsreiche
Quad-JFET-Opamp TL074 oder TL084 von
Texas-Instruments. Es spielt keine Rolle
welchen von diesen beiden Typen man einsetzt. Der einzige Unterschied
ist der, dass der TL074 rauschärmer ist, aber das spielt hier keine
Rolle. Beide Opamps sind gleich schnell in Bezug auf die
Unity-Gain-Bandbreite (Grenzfrequenz bei Verstärkung = 1) von 3 MHz und
die Slewrate (Anstiegsgeschwindigkeit) von 13 V/µS und vor allem darauf
kommt es hier an. Diese dynamischen Werte dieses Quad-Opamp genügen
für die vorliegende Anwendung.
Was tun IC:B1 und IC:B2? IC:B1 arbeitet als reiner Impedanzwandler mit
Verstärkung 1. Damit arbeitet der Spannungseingang Ue (e = eingang) für
die beiden Regelschaltungen sehr hochohmig, alleine bestimmt durch den
extrem hohen Eingangswiderstand der JFET-Eingangsstufe von IC:B1. Der
Ausgang von IC:B1 steuert die Regelschaltung für den Test der positiven
Ströme +Is. IC:B2 dient der Spannungsinversion mit einer Verstärkung von
-1, weshalb auch Widerstände mit einer Toleranz von 1 % im Einsatz sind.
Verwendet man JFET-Opamps, wie z.B TL084, benötigt man R6
selbstverständlich nicht. Der nichtinvertierende Eingang von IC:B2 kann
direkt mit GND verbunden werden. Bei der Verwendung eines bipolaren
Quad-Opamp dient R6 dazu, um den Eingangsstromdrift, bedingt durch
Temperaturänderungen, zu minimieren. Etwas mehr dazu liest man weiter
oben im Text zu Bild 4. Der Ausgang von IC:B2 steuert die negative
Stromsenke.
Wir kommen jetzt zum Steuer- und Schaltteil. Damit an P2 und P3 die
Widerstandswerte proportional zu den Spannungswerten sind, kommt eine
Konstantstromquelle zum Einsatz. Weil Konstantspannungsregler (7812,
7912) im Einsatz sind, darf die Konstantstromquelle den
Temperaturkoeffizienten nicht verschlechtern, weil sonst die Stabilität
der Strommessung ±Is verschlechtert wird. Eine Konstantstromquelle mit
Transistor und LED (5) eignet sich da eher
nicht. Alternativ dazu kommt eine Konstantstromquelle zum Einsatz, die
aus einer Bandgapspannungsreferenz Z (6),
einem Opamp IC:A und einem PNP-Transistor mit hoher Stromverstärkung
besteht. Diese Schaltung funktioniert genau so, wie die in Bild 4. Der
einzige Unterschied ist der, dass diese Stromquellenschaltung mit der
Betriebsspannung +12 VDC und nicht mit GND referenziert ist. Die
Polaritäten sind umgekehrt. Mit P1 (Trimmpotmeter) wird Iq auf 3.2 mA
abgeglichen. Dieser Strom erzeugt über P2 mit einem
Widerstandswert von 470 Ohm eine Spannung von 1.5 VDC. Mit dieser
Spannung fliesst der maximale Strom ±Is von ± 1.5A. Wenn die Toleranz
von P2 zu negativ ist, muss Iq mittels P1 etwas erhöht, im ungekehrten
Fall reduziert werden. Wichtig ist hier, dass ein Opamp zum Einsatz
kommen muss, der garantiert mit einer Eingangsspannung von 2.5 VDC
unterhalb der Betriebsspannung arbeitet.
Wie bereits erwähnt, Iq erzeugt über P2 eine Spannung von 1.5 VDC, wobei
der N-Kanal-MOSFET T2 offen sein muss. Durch P3 darf noch kein Strom
fliessen. P2 arbeitet potenziometrisch, d.h. mit dem Schleifer wird eine
Teilspannung Ue abgegriffen und der Stromtestschaltung zugeführt. Wenn
mittels positiver Schaltspannung Us T2 eingeschaltet wird, fliesst ein
Teil des Konstantstromes durch P3. Dieser Stromanteil ist vom
eingestellten Widerstand des P3 abhängig. Wird P3 auf 0 Ohm eingestellt,
wird mit Us die Spannung Ue zwischen dem an P2 einstellten Spannungswert
und praktisch 0 VDC (etwa 15 mVDC) umgeschaltet. Analog dazu wird ein
Strom ±Is zwischen einem bestimmten Wert und Null geschaltet. Wenn P2
auf maximalen Wert eingestellt ist, wird zwischen 150 mA (S2 = LOW) und
1.5 mA oder zwischen 1.5 A (S2 = HIGH) und etwa 15 mA umgeschaltet.
Befindet sich P3 auf Maximalwert, schaltet die Spannung Ue, bei
vorhandener Us-Rechteckspannung, stets im Verhältnis von 2:1 um, weil
die Widerstandswerte von P2 und P3 gleich gross sind. Wenn T2
ausgeschaltet ist, beträgt die Spannung über P2 1.5 VDC. Wird T2
eingeschaltet, wird bei maximalem Wert von P3 den gleich grossen
Widerstand zu P2 parallelgeschaltet und dies halbiert die Spannung über
P2, weil über dem halben Widerstandswert der gleich grosse Strom
fliesst. Dadurch wird die Spannung Ue und der Strom ±Is in einem
Verhältnis von 2:1 umgeschaltet, unabhängig davon welche Stellung der
Schleifer von P2 hat. Dieses Stromverhältnis bleibt sich gleich. Die
Einstellung von P2 dient einzig dem Stromwert von ±Is und die von P3
dient einzig dem Verhältnis des höheren zum niederen Stromwert.
Verändert man im Testeinsatz die Schleifereinstellung von P2, ändern
sich nur die beiden Stromwerte, jedoch nicht das Verhältnis der beiden
Stromwerte zueinander.
Warum man anstelle der Konstantstromquelle nicht einfach einen
Widerstand benutzt, hat damit zu tun, dass dieser Widerstand in die
Berechnung für die Umschaltung von Ue eingeht. Das ist bei einer
Betriebsspannung von 12 VDC zwar nicht besonders kritisch. Trotzdem
wollen wir dies mit Bild 7 kurz beleuchten:
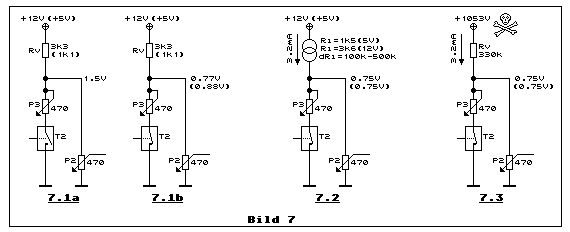
Teilbild 7.1a zeigt anstelle der Konstantstromquelle einen Vorwiderstand Rv mit einem Wert von 3.3 k-Ohm für +Ub = +12 VDC und 1.1 k-Ohm für +Ub = +5 VDC. In Teilbild 7.1a ist T2 - hier symbolisiert durch einen Schaltkontakt - offen. Es wirkt also nur P2 und die resultierende Spannung beträgt 1.5 VDC. Ist T2 (Teilbild 7.1b) geschlossen und P3 ist auf Maximalwert eingestellt, ist der Ausgangswiderstand, wegen Rv, grösser als die Hälfte des Wertes zuvor. Die Spannung beträgt bei +Ub = +12 VDC mit +0.77 VDC schon etwas mehr als die Hälfte von 1.5 VDC. Betreibt man diese Schaltung mit +Ub = +5 VDC sieht die Sache mit 0.88 VDC schon schlechter aus, weil Rv niederohmiger ist und daher mehr zum gesamten Widerstandsnetzwerk beiträgt. Fazit: Während die 12-VDC-Speisung für viele Anwendungen noch mit einfachem Vorwiderstand zulässig sein kann, besteht bei einer 5-VDC-Speisung eindeutig ein Problem. Wobei, es gibt nur dann ein echtes Problem, wenn die Widerstandswerte von P2 und P3 mit den Strömen und Stromverhältnissen linear korrelieren müssen, wie z.B. bei einer Verwendung von linearer Skalierung der Potmeter. Verwendet man eine Konstantstromquelle wie Teilbild 7.2 zeigt, hat man trotz relativ niederohmigem statischen Innenwiderstand von etwa 1.5 k-Ohm bei Ub = +5 VDC einen differenziellen Innenwiderstand im 100-k-Ohm-Bereich. Dies wäre, wie Teilbild 7.3 illustriert, etwa vergleichbar mit einer Spannung +Ub von mehr als 1000 VDC und Rv = 330 k-Ohm, und ganz ohne Witz, auf diese Weise baute man in der "Elektroniksteinzeit" Konstantstromquellen...
7. Technische Daten zu Bild 6
Test-Spannungsbereich Unt: ±4 VDC ... ±20 VDC (±Is = 1.5 A) ±3 VDC ... ±30 VDC (±Is = 0.5 A) ±2.5 VDC ... ±40 VDC (±Is = 0.1 A) (D1, D2 = Schottky-Dioden!) Test-Strombereich: 0 A ... ±1.5 A (P2 alleine) 0 A ... ±0.75 A (P2 + P1) Weiteres: Siehe Text! Maximale Taktfrequenz an Us: etwa 100 kHz Spannungswerte an Us: <0.5 V (T2 = aus) >2.1 V (T2 = ein), wenn besonders niederohmig, eher mehr Spannung. Eingangswiderstand an Us: 100 k-Ohm
8. Linkliste
- (1) Renovation eines "Steinzeit"-Netzgerätes
0.1 - 10 VDC / 3A
- (2) Komplementärdarlington-Transistorschaltung
(Theorie)
- (3) Einfaches Labornetzteil mit
NPN-Komplementärdarlingtonstufe und Überlastanzeige
- (4)
Darlington-Transistor (von Patrick Schnabel)
- (5) Die Transistor-LED-Konstantstromquelle
- (6) Z-Diode-Erweiterungskurs und die
Bandgap-Spannungseferenz