Das SC-Filter, eine kurze Einführung
Inhaltsverzeichnis
- Warum SC-Filter?
- Die CMOS-Geschichte in Kürze
- Nyquist, Shannon und der Wilde Westen
- Der RC- und der SC-Integrator
- Komplexere SC-Filter
- Clock, Abtastung und Non-Overlapping
- Das Tastverhältnis des Taktsignales
- Einfacher Non-Overlapping-Clockgenerator
- Das SC-Tiefpassfilter mit analogem Vor- und
Nachtiefpassfilter - Analoges Antialiasing-RC-Tiefpassfilter
- Analoges Smoothing-RC-Tiefpassfilter
- Steuerbares SC-Tiefpassfilter mit (steuerbaren)
analogen Filtern - Internet und Literatur zu SC-Filtern und Bauteile
- Ein paar Gedanken zum Schluss...
- Links zu weiteren SC-Filter-Elektronik-Minikursen
Warum SC-Filter?
Zeitkontinuierliche Filterschaltungen mit Operationsverstärkern (oder mit Transistoren), Widerständen und Kondensatoren werden rasch sehr aufwändig, wenn Ordnungszahl und/oder Filtergüte hoch sein müssen. Das ist dann nötig, wenn die Steilheit vom Durchlass- in den Sperrbereich - also in der Zone der Grenzfrequenz - sehr gross sein muss. Dazu kommt, dass bei hoher Ordnungszahl die Sensivität der Schaltung ebenfalls hoch ist. Dies bedeutet, dass die frequenzbestimmenden Widerstände und Kondensatoren sehr enge Toleranzen aufweisen müssen. Das kann schnell sehr teuer werden, besonders bei den Kondensatoren.
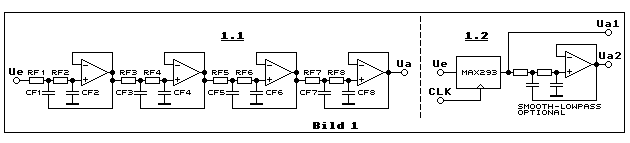
Teilbild 1.1 zeigt eine solche zeitkontinuierliche Filterschaltung. Es
ist ein Tiefpassfilter 8. Ordnung. Dies bedeutet, dass dieses
Tiefpassfilter acht frequenzbestimmende Widerstände (RF1...RF8) und
Kondensatoren (CF1...CF8) enthält. Will man die Grenzfrequenz mit einer
Spannung steuern und das erst noch in einem grossen Bereich, dann kann
man dies gleich vergessen. Der Aufwand wäre enorm gross, weil man muss
dabei auch diese Sensivität berücksichtigen. Man müsste die
frequenzbestimmenden Widerstände beispielsweise durch steuerbare JFETs
ersetzen und das scheitert, selbst bei gewisser aufwändiger
Linearisierung, noch immer am Linearitätsproblem. Reduziert man die
Spannungssteuerung auf eine Steuerung mit Potmeter, dann muss ein
Achtfachpotmeter eingesetzt werden. Man wird sehr grosse Mühe haben so
etwas mit genügend präzisem Gleichlauf überhaupt zu finden und eine
Spezialanfertigung kostet eine Riesenstange Geld.
Vergessen wir in so einem Fall lieber gleich alles und besorgen uns
ein zeitdiskretes Filter-IC, das nach dem Prinzip der geschalteten
Kondensatoren arbeitet. Ein sogenanntes Switched-Capacitor-Filter,
oder abgekürzt SC-Filter. Es gibt käufliche SC-Tiefpassfilter-ICs mit
unterschiedlichen Ordnungszahlen und mit unterschiedlichen
Filterdämpfungen (Güten). Es gibt SC-Tiefpassfilter, da kann man jeden
Parameter selbst definieren und es gibt kleine achtbeinige ICs mit
einer enormen Steilheit im Grenzfrequenzbereich von z.B. 100
dB/Oktave. Alle SC-Tiefpassfilter erfüllen locker die Forderung nach
grosser Frequenzvariation. Dies funktioniert mit einer Taktfrequenz die
meist 100 mal höher ist als die Grenzfrequenz. Ein solches
SC-Tiefpassfilter ist in Teilbild 1.2 als Blockschema skizziert. Als
SC-Tiefpassfilter mit hoher Steilheit im Bereich der Grenzfrequenz
käme beispielsweise ein MAX293 von Maxim oder ein LTC1064 von Linear
Technology in Frage.
Ein besondere Vorteil liegt im sehr guten Matching zwischen den einzelnen
SC-Filter-ICs des gleichen Typs. Wichtig ist dies z.B. beim Einsatz
einer Filterbank die mit einer Taktfrequenz gesteuert wird. Es ist
nämlich wichtig, dass man auf allen Übertragungskanälen mit den selben
SC-Tiefpassfilter-ICs die selben Laufzeiten bekommt. Dadurch sind die
Messwerte der einzelnen Kanäle untereinander vergleichbar.
Man sieht es, die Vorteile von SC-Filtern sind erschlagend und darum,
seit es diese SC-Filter gibt, sind sämtliche zeitkontinuierlichen
Filterschaltungen Schnee von vorgestern. Schön wär's, aber dem ist
nicht so. Nachteile hat auch das SC-Filter. Der Signal/Rausch-Abstand
ist schlechter, weil diese ICs mehr rauschen also hochwertige
Operationsverstärker (Opamp) mit niedrigen Rauschspannungsdichten in
zeitkontinuierlichen Filterschaltungen. Allerdings gibt es bei den
SC-Filtern auch Fortschritte. So ist das SC-Tiefpassfilter LTC1063
(Butterworth, 5. Ordnung) mit bloss 0.1 mVrms sehr rauscharm im
Vergleich zu andern SC-Filter-Produkten. Diese Rauschspannung enthält
auch den RMS-Wert der Clock-Feedthrough-Spannung.
Das SC-Filter ist ein abgetastetes System und darum erscheinen die
analogen Spannungen am Ausgang mit feinen Stufen. Stört dies, muss man
zusätzlich zeitkontinuierlich nachfiltern, was aber oft mit wenig
Aufwand erfolgen kann. Wie in Teilbild 1.2 angedeutet, genügt ein
einfaches aktives Tiefpassfilter zweiter Ordnung, dessen Grenzfrequenz
eindeutig über der Grenzfrequenz des SC-Tiefpassfilters liegen muss,
damit die 3-dB-Dämpfung bei der Grenzfrequenz des SC-Tiefpassfilters
nicht zusätzlich gedämpft wird. Oft genügt auch ein einfaches RC-Glied
zwischen dem Ausgang des SC-Filters und der nachfolgenden Schaltung.
Natürlich ist mit solchen zusätzlichen Massnahmen der steuerbare
Bereich der Grenzfrequenz der Filterschaltung eingeschränkt. Weitere
Ideen zu dieser Angelegenheit folgen im Elektronik-Minikurs
Steuerbares und steiles Tiefpassfilter in SC- und
Analog-Technik mit grossem Frequenzbereich.
Die CMOS-Geschichte in Kürze
1980 bis 1990 war das Jahrzehnt des CMOS. Dies verkündete Ende der
1970-Jahre Motorola mit Plakaten und Postern, und die Voraussage traf
zu. Die Morgendämmerung des allgemeinen CMOS-Siegeszuges begann
allerdings bereits mit der Motorola-CMOS-IC-Familie MC14xxx in der Mitte
der 1970er-Jahre. Beschleunigt wurde damals alles auch durch das
"McMOS-Handbook" von 1973 mit praxisnaher Einführung, guter Präsentation
des Innenlebens und der wichtigen Diagramme dieser CMOS-Familie. Dieses
Buch wurde damals von Motorola (Omni-Ray Schweiz) an alle
elektrotechnischen Institute der ETH-Zürich in grossen Mengen gratis
abgegeben.
Die Möglichkeit diese digitalen ICs bis zu 15 VDC zu speisen, bietet ein
ein hohes Mass an Störimunität und Dynamik, weil dadurch das Verhältnis
der maximal aussteuerbaren Signalspannung zur Rausch/Stör-Spannung
besonders hoch ist. Dies wirkt sich ganz besonders vorteilhaft bei
digital steuerbaren
analogen Schaltern,
die es ebenfalls in dieser CMOS-Familie (z.B. MC14066) gibt, aus. Aber
auch für digitale Steuerschaltungen, denn bei höheren Logikpegeln ist
das Störrisiko durch artfremde Spikes überproportional zur
Pegeldifferenz geringer.
Trotz der heutigen Vielfalt an programmierbaren digitalen Bausteinen,
wie PLDs bis hin zu modernen Controllern und DSPs, ist diese
CMOS-Familie von Motorola nicht ausgestorben. Etwa zur selben Zeit hatte
National-Semiconductor die CMOS-Familie CD4xxx in ihr Programm
aufgenommen. Diese beiden CMOS-Familien sind anschlusskompatibel und
elektrisch kompatibel. Die Bezeichnungen haben ein gemeinsames System,
das man leicht mit einem Beispiel erkennt: Der obengenannte Analogswitch
MC14066 von Motorola heisst bei National-Semiconductor CD4046. Oder das
Dual-Monoflop-IC heisst bei Motorola MC14538 und bei
National-Semiconductor CD4538.
Der Einsatz dieser beiden CMOS-Familien macht vor allem dort Sinn, wo
die digitale und die analoge Welt sich verbindet, wenn grössere
Betriebsspannungen als nur 3.3 VDC oder 5 VDC, z.B. wegen obergenannter
Dynamik und Störimmunität, notwendig ist.
Das Jahrzehnt des CMOS brachte ein Produkt hervor, welches eine Art
Zwischenwelt von Analog und Digital ist. Es ist das SC-Filter. Davon
wird hier und in den folgenden Elektronik-Minikursen zum selben Thema
berichtet. Siehe
Indexseite
unter SC-Filter-Schaltungen. Hier befassen wir uns etwas mit den
Grundlagen und dazu unternehmen wir auch eine Reise in das Innenleben
des fundamentalen Aufbaus von SC-Filterbausteinen. Zunächst streifen wir
das Thema über abgetastete Systeme, womit man es bei A/D- und
D/A-Wandlern, aber auch bei SC-Filtern zu tun hat. Es gibt seit den
frühen 1980er-Jahre auch A/D-Wandler die, anstelle der traditionellen
Widerstands-, SC-Netzwerke enthalten. Dies sei hier bloss am Rande
erwähnt...
Nyquist, Shannon und der Wilde Westen
Beginnen wir mit dem Wilden Westen und erinnern uns an einen alten
Hollywoodstreifen in Schwarzweiss. Gemächlich fährt eine mit Geld
beladene Postkutche auf einer staubigen Strasse durch die Prärie. Das
Geld in der Postkutsche ist für die Lohnzahlungen der Bauarbeiter einer
neuen Eisenbahnlinie bestimmt. Ob dieses Geld jemals das Ziel erreichen
wird, bleibt offen, denn ein paar "schräge Vögel" mit Pferden hinter
einem Hügel lauernd, beobachten schon eine Weile diese Postkutche. Dann
laden sie ihre "Knarren", schwingen sich auf die Pferde, die schwarze
Maske über ihre Gesichter und dann geht's mit Tempo los in Richtung
Postkutsche. Der Kutscher bemerkt dies und treibt seine Pferde an, die
als wie schneller rennen. Der Film zeigt immer wieder die Räder und das
Wegstäuben des Sandes, um den Eindruck der hohen Geschwindigkeit zu
vermitteln. Je näher die Räuber kommen, um so heftiger treibt der Fahrer
die Kutschenpferde an. Die Räder drehen als wie schneller, aber dann
bemerken die Kinobesucher plötzlich, wie die Räder als wie langsamer
drehen. Sie beobachten dies an den Radspeichen. Die Räuber kommen noch
näher, der Kutscher beschleunigt zusätzlich und plötzlich sieht man wie
die Räder scheinbar stillstehen. Der Kutscher versucht, wenn auch
vergebens, vor den Räubern zu fliehen und gibt den Pferden noch einmal
die Sporen. Die Kutsche fährt noch etwas schneller, die Kamera zeigt
erneut die Räder und die drehen jetzt für den Kinobetrachter eindeutig
rückwärts. Was passiert da eigentlich? Nur dies soll uns jetzt weiter
interessieren, was mit dem Postkutscher und mit dem Geld geschah, ist
eine ganz andere Geschichte...
Wenn man die zunehmende Drehzahl eines Rades direkt beobachtet, sieht
man die Realität. Oberhalb einer gewissen Drehzahl können wir
natürlich eine Änderung, auf Grund der Trägheit des Auges, nicht mehr
wahrnehmen. Wir haben es mit einem zeitkontinuierlichen Vorgang zu tun.
Wenn man jedoch mittels eines Filmes, mit einer gewissen Anzahl von
Bildern pro Sekunde, Geschehnisse beobachtet, haben wir es mit einem
zeitdiskreten Vorgang zu tun und das wirkt sich folgendermassen aus:
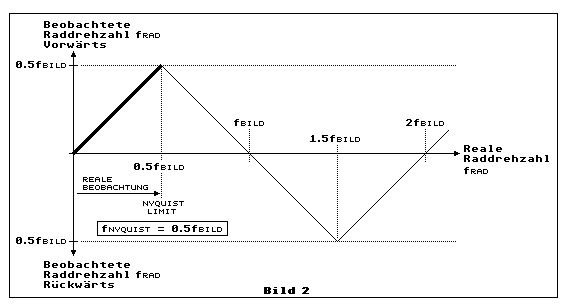
Bis zur halben Bildfrequenz beobachtet man die Wirklichkeit. Die
bebachtete Drehzahl des Rades (Radfrequenz) entspricht der wirklichen
Drehzahl. Erhöht sich die Drehzahl weiter bis zur Bildfrequenz, nimmt
die beobachtete Drehzahl ab bis zum scheinbaren Stillstand. Bei weiterer
Zunahme bis zur 1.5-fachen Bildfrequenz, beobachtet man erneut eine
Zunahme der Drehzahl, aber das Rad dreht scheinbar rückwärts. Noch
schneller bis zur doppelten Bildfrequenz nimmt die scheinbare Drehzahl
des scheinbar rückwärtslaufenden Rades wieder ab bis zum Stillstand.
Oberhalb der doppelten Bildfrequenz beginnt das Ganze von Neuem. Wichtig
dabei ist noch, dass das Rad real zwar immer schneller dreht, der
Beobachter sieht jedoch immer nur eine Geschwindigkeitsänderung zwischen
Null und der halben Bildfrequenz und dies von dem Augenblick da das
sogenannte Abtastheorem verletzt wird (Nyquistgrenze). Genau das ist der
Fall, wenn die Drehzahl des Rades die halbe Bildfrequenz überschreitet.
Dadurch, dass auf der Y-Achse die beobachtete Drehzahl und die
beobachtete Drehrichtung aufgetragen ist, zeigt sich das Diagramm
dreieckförmig.
Was genau sagt uns dieses Abtasttheorem, bzw. das Nyquistkriterium oder
die Nyquistgrenze, im Bereich der Elektronik? Es sagt uns, dass eine
abgetastete, elektronische Schaltung (z.B. A/D- oder D/A-Wandler) keine
höhere Signalfrequenz als die halbe Abtastfrequenz korrekt verarbeiten
kann. Ein praktisches Beispiel mit einer Blockschaltung, bestehend aus
Mikrofon, Verstärker (V), Antialiasing-Tiefpassfilter (TP-FILT.) und
A/D-Wandler, zeigt Teilbild 3.1:
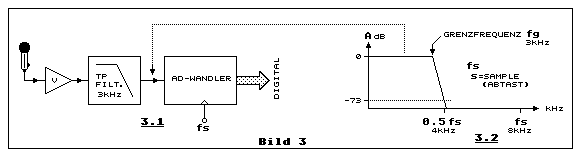
Die menschliche Sprache hat eine Frequenzbandbreite von etwa 10 kHz,
vielleicht auch etwas mehr (Zischlaute). Wird die Sprache bei der
Digitalisierung mit bloss 8 kHz abgetastet, würden Sprachfrequenzanteile
die höher sind als die halbe Abtastfrequenz (4 kHz), in den unteren
Frequenzbereich gefaltet. Dadurch bilden sich Differenzfrequenzen
(Aliasfrequenzen) die im Bereich der Sprachfrequenz liegen, aber in
Wirklichkeit gar nicht existieren. Die Sprache hört sich seltsam an.
Dieser unerwünschte Effekt wird vermieden, in dem das Sprachsignal in
seiner Frequenzbandbreite so stark bandbegrenzt wird, so dass nur noch
vernachlässigbar geringe Signalanteile oberhalb der halben
Abtastfrequenz das abgetastete System erreichen. Damit fällt der
Faltungs-, bzw. Aliaseffekt vernachlässigbar gering aus.
Dazu verwendet man Tiefpassfilter. Je steiler die Amplitude im
Grenzfrequenzbereich abfällt, je näher kann die Filtergrenzfrequenz an
die Nyquistgrenze (halbe Abtastfrequenz) dimensioniert werden. Dies
bedeutet, dass man die Abtastfrequenz so niedrig wie möglich halten kann
oder man nützt eine maximal mögliche Frequenzbandbreite des
Sprachsignales aus. Eine möglichst niedrige Abtastfrequenz bedeutet bei
der digitalen Aufzeichnung minimaler Verbrauch an Speicherplatz. Das
Diagramm in Teilbild 2.2 illustriert ein Beispiel, bei dem das
Sprachsignal bei der halben Abtastfrequenz mit 73 dB gedämpft wird. Dies
entspricht etwa dem Quantisierungsrauschabstand eines
12-Bit-A/D-Wandlers.
Damit beenden wir das Thema Abtastung, Nyquist/Shannon-Abtasttheorem,
und Anti-Aliasing in den Grundlagen. Wer mehr dazu erfahren und sich
vertiefen möchte, empfehle ich das Kapitel "Digitale Filter" im Buch
Halbleiter-Schaltungstechnik von U.Tietze und Ch. Schenk. Für das
Verständnis der weiteren Elektronik-Minikurse zum Thema SC-Filter
genügen jedoch diese Grundlagen.
Der RC- und der SC-Integrator
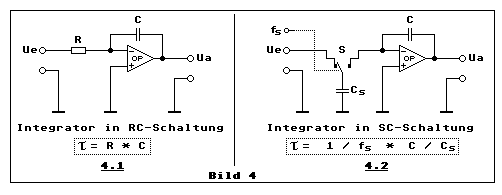
Teilbild 4.1 zeigt den typischen, zeitkontinuierlichen analogen
Integrator. Die Zeitkonstante kann durch die Variation von R oder C
verändert werden. Teilbild 4.2 zeigt einen zeitdiskreten Integrator der
nach dem Switched-Capacitor-Prinzip (SC-Prinzip) arbeitet. Anstelle des
Widerstandes R wirkt hier der umschaltende elektronische Schalter S mit
dem Kondensator Cs. Diese beiden Komponenten übernehmen mit der
Abstastfrequenz fs, die den Schalter S steuert, die Aufgabe des
Widerstandes R. Der Wert dieses simulierten Widerstandes ist durch fs
steuerbar. Genau dies zeichnet das Besondere an SC-Filtern aus: Je höher
die Abtastfrequenz fs und ebenfalls, je höher die Kapazität des
Kondensator Cs, um so niedriger ist der simulierte Widerstand R und
ebenso niedriger die resultierende Zeitkonstante, gegeben aus diesem
simulierten Widerstand R und dem Integrator-Kondensator C. Die
Abtastfrequenz ist mit fs bezeichnet, weil im Englischen die
Abtastfrequenz mit Sample-Frequency (s für sample) bezeichnet wird. Die
Bezeichnung Sample - auf deutsch Probe - kommt davon, weil bei
der Abtastung Proben des analogen Signals entnommen, gespeichert und
verarbeitet werden.
In der Betrachtungsweise eines SC-Tiefpassfilters gilt folgendes: Die
Grenzfrequenz ist reziprok zur Zeitkonstante, und das bedeutet, je höher
die Abstastfrequenz, um so höher die Filtergrenzfrequenz. Die Formel in
Teilbild 4.2 zeigt, dass die Zeitkonstante, bzw. Grenzfrequenz, nicht
mehr wie beim analogen Integrator in Teilbild 4.1, nur von einer
Kapazität C abhängig ist. Sie ist abhängig vom Verhältnis der beiden
Kapazitäten C/Cs. Da beide Kapazitäten auf dem selben Siliziumchip
integriert sind, deshalb beide den selben Temperaturkoeffizienten haben
und ebenso den selben Temperaturunterschied erfahren, wirken sich
Temperaturunterschiede auf die Filterparameter kaum aus. Das Verhältnis
von C/Cs bestimmt auch direkt das Verhältnis von der Abtastfrequenz fs
zur Filtergrenzfrequenz fg.
Dieses Verhältnis legt der IC-Hersteller meist mit 25, 50 oder 100 fest.
Die Toleranz beträgt etwa ±1% oder weniger. Es ist wichtig, dass dies
dem Anwender bewusst ist, denn diese Verhältniszahl ist nicht etwa eine
fixe digitale Grösse, wie manche Einsteiger in die praktische
SC-Filtertechnik manchmal glauben. Dass es zur Berechnung der
Zeitkonstante, bzw. Grenzfrequenz, keinen absoluten Kapazitätswert
bedarf, hat noch einen andern wichtigen Vorteil: Es ist sehr schwierig
auf einem Siliziumchip Kondensatoren mit niedrigen Kapazitätstoleranzen
herzustellen. Erzeugt man jedoch gleich zwei Kondensatoren auf dem
selben Chip, dann weisen beide Kondensatoren praktisch dieselbe Toleranz
auf. Auf diese Weise neutralisieren sich die Toleranzen beider
Kondensatoren weitgehend.
Die absolute Grösse der Kapazitäten spielt allerdings auch eine gewisse
Rolle. Gelingt es nämlich grosse Kapazitätswerte zu integrieren und
diese mit genügend Strom schnell genug zu treiben - hier sind die
integrierten Opamps herausgefordert - erreicht man ein geringeres
SC-Filterrauschen. Daraus resultiert ein höherer Signal/Rausch-Abstand.
Dieser liegt in der Regel zwischen 70 und 80 dB. Diese Rauschspannung
darf keinesfalls mit dem Clockfeedthrough-Störspannung verwechselt
werden. Doch dazu später mehr.
Komplexere SC-Filter
Wie verlassen nun diesen einfachen Integrator und wenden uns hin zu den seit etwa anfangs der 1980er-Jahren käuflichen integrierten SC-Filtern, die es teils weiterentwickelt auch noch heute gibt. Ich schätze, Maxim und Linear-Technology sind momentan (2007) wohl die beiden führendsten Herstellerfirmen auf diesem Gebiet. In der Frühphase der Entstehung käuflicher integrierter SC-Filter war die Firma Reticon der Pionier und glänzte, für die damalige Zeit, mit hochwertigen Produkten. Reticon produzierte schon damals ein SC-Tiefpassfilter mit der enormen Steilheit im Grenzfrequenzbereich von 100 dB/Oktave und dies mit sehr geringen relativen Rippelspannungswerten von etwa 0.1 dB im Durchlassbereich und dies in einem kleinen DIL-8pin-Gehäuse. Es war der R5609, der schon sehr lange nicht mehr hergestellt wird. Dafür gibt es heute (2007) von Maxim den vergleichbaren Typ MAX293, ebenfalls in einem DIL-8pin-Gehäuse. Er ist jedoch nicht pinkompatibel zu R5609. Mit einem selbstrealisierten kleinen Adapterprint jedoch leicht austauschbar.
Clock, Abtastung und Non-Overlapping

Aus dem Kapitel Nyquist, Shannon und der Wilde Westen wissen wir
jetzt was es mit dem Abtasttheorem auf sich hat und damit haben wir auch
hier zu tun. Der Nachteil des abgetasteten Systems ist hier nicht so
kritisch wie z.B. bei einem AD-Wandler ohne Oversamplingeigenschaft,
weil das Verhältnis zwischen der Abtast- und der Grenzfrequenz in der
Regel sehr gross ist. Aber Vorsicht! Es gibt einen Stolperstein. In den
Datenblättern von SC-Tiefpassfiltern steht meist etwas von einem
Clock/Cutoff-Frequency-Ratio, also dem Verhältnis zwischen der
Taktfrequenz und der Filtergrenzfrequenz. Diese Taktfrequenz - auch
Clockfrequenz genannt - am Eingang CLK ist aber meist doppelt so gross
wie die eigentliche Abtastfrequenz fs. Dies kommt daher, weil es IC-intern
oft einen 1:2-Frequenzteiler (D-FF) hat. Mit D-FF wird hier ein
Frequenzteiler 1:2 mittels /Q-D-rückgekoppeltem D-Flipflop symbolisch
angedeutet. Grundsätzlich ist es einfach ein Toggle-Flipflop.
Nehmen wir als praktisches Beispiel das SC-Tiefpassfilter MAX293 von
Maxim mit seiner Clock-to-cutoff-frequency-ratio von 100:1, dann beträgt
das eigentliche Verhältnis von der Abtast- zur Grenzfrequenz bloss 50:1
und das Verhältnis von der Nyquistgrenze zur Grenzfrequenz 25:1. Mit
andern Worten, das Abtasttheorem wird verletzt, wenn das
Frequenzspektrum des Eingangssignales Ue höhere Frequenzanteile als ein
Viertel der Taktfrequenz am Eingang CLK hat.
Die Integration des 1:2-Frequenzteiler (D-FF) ist sehr vernünftig, weil
das Tastverhältnis der Abtastfrequenz fs am Ausgang des Frequenzteilers
(D-FF) in der Regel exakt 0.5 sein muss. Der Anwender hat mit diesem
integrierten Toggle-Flippflopp den Vorteil, dass man sich nicht um
dieses Tastverhältnis kümmern muss. Der Takteingang CLK ist entweder
positiv oder negativ flankengetriggert. Mit dem präzisen Tastverhältnis
von 0.5 für das SC-Filter ist es alleine allerdings noch nicht getan.
Nicht weniger wichtig ist die sogenannte Non-Overlappingschaltung
(NON-OVERLAPP) mit den beiden Phasenausgängen P und /P (P für Phi). Das
Non-Overlapping sorgt dafür, dass der integrierte elektronische
CMOS-Schalter
S immer zuerst ganz offen ist, bevor einer der beiden Kontakte
überbrückt wird. Man nennt dies auch "breaking before making" und man
beachte dazu in Bild 5 das Impulsdiagramm der Abtastfrequenz
fSAMPLE mit P und /P. Die kurzen Zeiten bei denen P
und /P gleichzeitig auf LOW-Pegel sind, sind die
Nichtüberlappungszeiten. Während dieser kurzen Zeit sind beide Kontakte
von S offen.
Wozu benötigt es zwischen den Flanken von P und /P eine kurze
Nichtüberlappungszeit? Ohne diese wäre der Eingang Ue mit dem
invertierenden Eingang des Opamp kurzzeitig kurzgeschlossen. Ue wäre
also direkt mit dem invertierenden Eingang des Opamp verbunden. C wäre
kurzzeitig mit der niederohmigen Quelle Ue gekoppelt. Dadurch würde die
Schaltung nicht mehr funktionieren.
Die korrekte Arbeitsweise mit der Nichtüberlappungszeit: Zuerst ist P
auf logisch HIGH und Cs wird vom Pegel an Ue geladen. Beim
Umschaltvorgang, P und /P auf logisch LOW, ist Cs während dieser
Nichtüberlappungszeit von beiden Kontakten kurz getrennt. Danach wird /P
logisch HIGH und die Ladung von Cs überträgt sich teilweise auf C. Die
minimale Nichtüberlappungszeit ergibt sich aus den realen
Flankensteilheiten der beiden Logiksignale P und /P. Die maximale
Abtast- bzw. Taktfrequenz ist davon ebenso definierbar.
Man spricht bei SC-Filtern von zwei Phasen des digitalen Abtastsignals.
Das ist im Prinzip nicht ganz richtig, weil die beiden Signale P und /P
durch Inversion erzeugt werden. Warum dies ein Unterschied ist, wird im
Elektronik-Minikurs
Amplifier-Attenuator
im Kapitel "Phasenverschiebung oder Inversion, das ist hier die
Frage" ausführlich erklärt. Allerdings ist die Erklärung dort mit
analogen Signalen nicht so einfach in die digitalen Vorgänge hier
übertragbar. Es gab in der Pionierzeit der SC-Filtertechnik
Experimentierschaltungen bei denen man nicht nur Zweiphasen-, sondern
sogar Mehrphasen-Abtastsignale einsetzte. Diese wurden mittels digitalen
Schieberegistern oder Zählern erzeugt. Weil dabei z.B. ein HIGH-Pegel
von einem Schieberegister- oder decodierten Zählerausgang zum nächsten
durchgeschaltet wird, ist der Phasenbegriff eher angebracht. Naja, man
könnte darüber bestimmt ausgiebige Diskussionen veranstalten. Wem es
Spass macht...
Das Tastverhältnis des Taktsignales
Das SC-Tiefpassfilter MAX293 hat einen intergrierten 1:2-Frequenzteiler.
Dies hat den Vorteil, dass der Anwender sich nicht um das Tastverhältnis
des Taktsignales kümmern muss. Es können sowohl Rechtecksignale als auch
feine Nadelimpulse sein, sofern die minimale Impulsbreite des
IC-internen T-Flipflop eingehalten wird. Es gibt aber noch sehr viele
andere SC-Tiefpass- und SC-Universalfilter, vor allem die der älteren
Generation, welche keinen integrierten 1:2-Frequenzteiler beinhalten.
Bei diesen ICs gilt natürlich Taktfrequenz gleich Abtastfrequenz. Das
Verhältnis von der Nyquistgrenze zur Grenzfrequenz beträgt dann nicht
25:1, sondern 50:1, wenn das Verhältnis von Taktfrequenz zu
Grenzfrequenz, wie üblich, 100:1 ist.
Man muss in diesem Fall auch darauf achten, dass das Tastverhältnis
beim Taktsignal (oft) 0.5 betragen muss. Es gibt aber auch Ausnahmen,
wie beim LTC1063. Dass dieses SC-Tiefpassfilter kein 1:2-Frequenzteiler
beinhaltet, erkennt man daran, dass das Tastverhältnis des Taktsignales
zwischen 0.3 und 0.5 liegen darf. In den Datenblättern sind Angaben
darüber, ob es intern einen 1:2-Frequenzteiler hat oder nicht, oft sehr
dürftig und unklar. So kommt man schlichtweg nicht drum herum, vor
einem Schaltungsdesign, zuerst mit einem kleinen Versuchsaufbau, sich
Gewissheit zu verschaffen. Dies lohnt sich sowieso, wenn man ein neues
SC-Filter-IC kennenlernen will. Den Inhalten der Datenblätter und
Applicationnotes darf man nicht blind vertrauen.
Einfacher Non-Overlapping-Clockgenerator
In den Pioniertagen von SC-Filtern realisierte man diese quasidiskret mittels integrierten CMOS-Analogschaltern, Opamp, Kondensatoren, etc. und man musste natürlich auch die Nichtüberlappungsschaltung selber aufbauen - wobei dies sehr einfach sein kann, wie dies die Schaltung in Bild 6 illustriert:
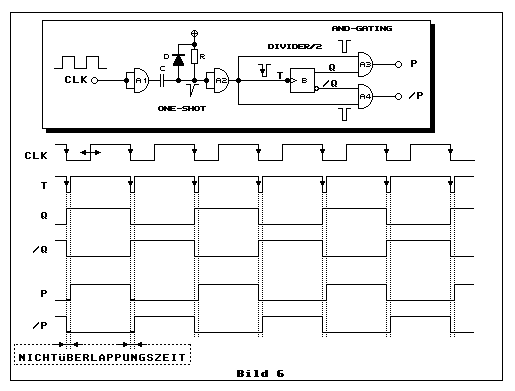
Mit einer ONE-SHOT-Schaltung, bestehend aus den beiden AND-Gates IC:A1
und IC:A2, werden aus einem Rechtecksignal mit einem Tastverhältnis von
0.5 am Eingang CLK, aus den fallenden Flanken, kurze "negative" Impulse
generiert. Im Augenblick der fallenden Flanke an CLK, erfolgt eine
ebensolche am Ausgang von IC:A1. Kondensator C ist zunächst entladen. C
wird aber sogleich durch R bis maximal zur Betriebsspannung aufgeladen.
Etwa bei der halben Betriebsspannung am Eingang von IC:A2 schaltet
dessen Ausgang von LOW zurück auf HIGH. Wenn die Eingangsspannung eines
CMOS-Gatters auf halber Betriebsspannung liegt, arbeitet das Gatter in
einem quasilinearen Bereich mit einer hohen Verstärkung. Dies hat zur
Folge, dass die relativ flache Ladekurve von C durch diese hohe
Verstärkung am Ausgang von IC:A2 derart viel steiler wird, so dass die
maximale Flankensteilheit des Gatters die Flankensteilheit des Signals
begrenzt. Dies bedeutet natürlich, dass die Zeitkonstante R*C nicht
beliebig gross sein darf. Ist diese zu gross, reicht die hohe
Verstärkung zur Bildung einer hohen Flankensteilheit nicht aus und dies
führt in der Regel zu unkontrollierten Schwingungen am Ausgang des
IC:A2. In diesem Fall müssen (N)AND-Schaltungen mit Eigenschaften von
Schmitt-Triggern eingesetzt werden. Bei dieser Anwendung hier benötigt
man allerdings nur R*C-Zeitkonstanten in der Grössenordnung von 50 bis
200 ns und dafür reicht auch für IC:A2 ein einfaches CMOS-AND-Gatter.
Die Diode D sorgt dafür, dass C, bei ansteigender Flanke am Ausgang von
IC:A1, sofort entladen wird. Die Entladezeit ergibt sich hauptsächlich
aus C, dem sehr niedrigen dymamischen Innenwiderstand der Diode D und
dem Innenwiderstand der CMOS-Ausgangsstufe von IC:A1. Die Restentladung
unterhalb der Dioden-Schwellenspannung besorgt Widerstand R.
Diese kurzen Impulse dienen sowohl der Nichtüberlappungszeit, als auch
zur Frequenzteilung mittels Toggle-Flipflop DIVIDER/2 (IC:B). Die
fallende Flanke an T schaltet das Flipflop IC:B jeweils um. Die beiden
umgeschalteten Pegel an Q und /Q werden jedoch nicht sofort mittels der
beiden Gatter IC:A3 und IC:A4 zu den beiden Phasen-Ausgängen P und /P
durchgeschaltet. IC:B hat eine sehr kurze Laufzeitverzögerung, aber
diese bewirkt, dass vor der Übetragung von Q und /Q nach P und /P beide
AND-Gates durch den kurzzeitigen LOW-Pegel des Impulses gesperrt
(disabled) werden. Dieses Disabling - so nennt man dies bei Flipflops -
muss während der ganzen Umschaltphase, und etwas mehr, andauern. So wird
garantiert, dass beide Phasen-Ausgänge P und /P während dieser kurzen
Impulsdauer sicher auf LOW bleiben. Dies ist die Nichtüberlappungszeit.
Das SC-Tiefpassfilter mit analogem Vor- und Nachtiefpassfilter
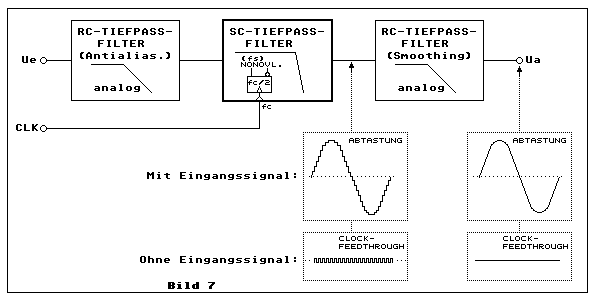
Bei einer SC-Tiefpassfilterschaltung kann der Begriff Antialiasing zweimal vorkommen. Einmal, wie bereits weiter oben angedeutet, wenn das SC-Tiefpassfilter selbst als Antialiasing-Tiefpassfilter vor ein abgetastetes System (A/D-Wandler) geschaltet wird. Ein andermal, wenn vom SC-Tiefpassfilter selbst die Rede ist. Da auch dies ein abgetastetes System ist, wird wenigstens ein einfaches analoges passives RC-Tiefpassfilter erster Ordnung dem Eingang des SC-Tiefpassfilters als Antialiasing-Tiefpassfilter vorgeschaltet, wie dies Bild 7 oben links andeutet. Das selbe gilt betreffs Smoothing-Tiefpassfilter, das die feinen Spannungsstufen glättet. Die gesamte Prinzipschaltung in Bild 7 kann man als Antialiasing-Tiefpassfilter vor einen A/D-Wandler oder als Smoothing-Tiefpassfilter nach einem D/A-Wandler einsetzen.
Analoges Antialiasing-RC-Tiefpassfilter
Dieses und die folgenden Kapitel beziehen sich immer wieder auf die
beiden Bilder
7
und
8.
Es empfiehlt sich, zum weiteren Studium, diese Bilder separat anzuzeigen
oder auszudrucken.
Ohne ein solches Tiefpassfilter würden Frequenzen des analogen
Eingangssignales oberhalb der halben SC-Filter-Abtastfrequenz in den
Übertragungsbereich gefaltet. Dudurch treten im Nutzfrequenzbereich
Signale auf, die in Wirklichkeit nicht existieren, wie bereits weiter
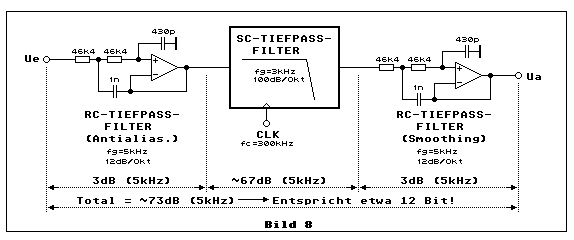
oben beschrieben. Da jedoch die halbe Abtastfrequenz bei einem
SC-Tiefpassfilter bei fc/fg=100 25 mal höher ist als die
effektive Bandbreite fg des analogen Eingangsignales, genügt es oft ein
passives analoges Tiefpassfilter erster Ordnung (einfache RC-Schaltung)
einzusetzen. Für wesentlich bessere Signalqualität empfiehlt sich jedoch
ein aktives Butterworth-Tiefpassfilter zweiter Ordnung vorzuschalten,
wie dies Bild 8, links vom SC-Tiefpass-Filter, illustriert:
Analoges Smoothing-RC-Tiefpassfilter
Weiter oben wurde am Beispiel eines D/A-Wandlers erwähnt, dass das
Ausgangssignal auf Grund des Abtastens stufenförmig erfolgt. Dies trifft
natürlich ebenso auf den Ausgang eines SC-Filters zu - allerdings ist
die Stufenauflösung wesentlich feiner. Man muss die Frequenz des
Eingangssignales schon bis in die Nähe der eingestellten Grenzfrequenz
des SC-Tiefpassfilters fahren, um die Stufenform mit einem Oszilloskopen
überhaupt zu erkennen. Das analoge Smoothing-Tiefpassfilter, mit den
selben Parametern wie das im obigen Kapitel genannte analoge
Antialiasing-Tiefpassfilter, glättet diese Stufenform. Man
vergleiche die beiden Sinussignale, eines vor und eines nach dem
analogen Smoothing-Tiefpassfilters in Bild 7.
Es gibt aber noch ein anderes Problem, weshalb dieses
Smoothing-Tiefpassfilter nicht fehlen sollte. Jedes SC-Filter erzeugt am
Ausgang ein sogenanntes Clockfeedthrough-Störsignal. Dieses tritt auch
ohne Eingangssignal in Erscheinung und existiert synchron zur
Abtastfrequenz des SC-Tiefpassfilters mit einer Spannung bis etwa 10
mVpp oder auch etwas mehr mehr.
Dieses abgeschwächte "Durchdrücken" des Abtastsignales kommt durch die
sogenannte Ladungsinjektion der CMOS-Analogschalter zustande, welche die
Cs-Kapazitäten (Bilder 3 und 4) umschalten. Diese Störspannung ist
weitaus grösser als die vom SC-Filter erzeugte Rauschspannung. Zum Glück
fällt das Clockfeedthrough-Störsignal nur wenig in's Gewicht, weil die
Frequenz weit ausserhalb der Grenzfrequenz des SC-Tiefpassfilters liegt.
Damit sich diese Clockfeedthroughstörspannung nicht auswirken kann, muss
auch diese Störspannung mit dem analogen Smoothing-Tiefpassfilter
unterdrückt werden. Tut man dies, misst man am Ausgang nur noch die zu
erwartenden SC-Filter-Rauschwerte, wenn kein Eingangssignal vorliegt.
Noch einmal zusammengefasst: Mit dem analogen Smoothing-Tiefpassfilter
am Ausgang des SC-Tiefpassfilters schlägt man zwei Fliegen auf einen
Schlag: Erstens glättet man die feinen Stufen des Ausgangssignales,
welche durch die SC-Filterabtastung zustande kommen und zweitens
unterdrückt man das abtastfrequenzsynchrone Clockfeedthrough-Störsignal.
Steuerbares SC-Tiefpassfilter mit (steuerbaren) analogen Filtern
Benutzt man ein SC-Antialiasing-Tiefpassfilter mit variabler Grenz-,
bzw. Takt- und Abtastfrequenz in einem grossen Bereich, muss natürlich
auch die Grenzfrequenz des analogen Antialasing- und des analogen
Smoothing-Tiefpassfilters synchron nachgeführt werden. Ein solches
analoges Tiefpassfilter realisiert man dann vorzugsweise mit einem
strom-, bzw. spannungssteuerbaren OTA (Operational Transconductance
Amplifier) und einem einfachen Frequenz/Spannungs-Converter, der die
Taktfrequenz in eine Steuerspannung umsetzt. Bei nur geringer
Grenzfrequenzvariation genügen allerdings fix dimensionierte analoge
Butterworth-Tiefpassfilter zweiter Ordnung, wie dies weiter oben Bild 8
illustriert.
Mit Bild 8 setzt der nachfolgende Elektronik-Minikurs mit dem Titel
SC-Tiefpassfilter-Einheit mit umschaltbaren
Grenzfrequenzen
das Thema SC-Filter fort.
Internet und Literatur zu SC-Filtern und Bauteile
Man findet reichlich Informationen über SC-Filter via
Internet-Suchmaschinen. Es lohnt sich auch englische Wörter kombiniert
einzugeben, da es wesentlich mehr englischsprachige Webseiten zu diesem
Thema gibt.
Die "Elektronik-Bibel" Halbleiter-Schaltungstechnik von U.Tietze
und Ch. Schenk (9. Auflage) bietet einiges an Grundlagen über SC-Filter.
Der Haupttitel nennt sich "Switched-Capacitor-Filter". Es gibt dazu
folgende Untertitel: "Grundprinzip", "der SC-Integrator", "SC-Filter
erster Ordnung", "Entwurf von SC-Filtern zweiter Ordnung", "Integrierte
Realisierung von SC-Filtern", "Allgemeine Gesichtspunkte beim Einsatz
von SC-Filtern" und es gibt eine ganze Seite mit dem Titel
"Typenübersicht". Diese enthält Universalfilter, Tiefpässe, Hochpässe,
Bandpässe und Sperrfilter. Allerdings möchte ich beifügen, dass man die
Reticon- und Thomson-Produkte vergessen muss. Es gibt sie nicht mehr.
Von den Herstellern der SC-Filter-ICs gibt es Bücher (und Links) mit
Grundlagen und Application-Notes. Nennswert sind die Firmen
Maxim
und
Linear Technology.
Ein paar Gedanken zum Schluss...
So mancher mag sich fragen, wozu man solche Filtersysteme überhaupt noch
braucht, man lebt heute doch im Zeitalter von digitalen Filtern, DSP und
Oversampling. Diese kritische Anmerkung ist durchaus berechtigt -
nämlich dann, wenn man es in einem Gesamtsystem mit der Digitalisierung
nicht übertreibt.
Man übertreibt es allerdings, wenn man pro Kanal grosse
Frequenzbandbreiten, viele simultane Kanäle, bei allen Kanälen möglichst
steilflankige Digitalfilter und ebenfalls noch Spezialfilter wie
Bandpass-, Sperrfilter us.w. haben möchte. Dann kommt ein rein digitales
System bald einmal an seinen Limit. So etwas habe ich mit einem
käuflichen volldigitalisierten sehr teuren medizinischen
EMG-Datenerfassungsgerät miterlebt, als der Hersteller sich an Ort
bemühen musste, um einen schnelleren Prozessor einzubauen. Das kann sich
in Zukunft mit noch schnelleren digitalen Systemen zu Ungunsten
von SC-Filtern erheblich verbesseren.
Manchmal ist es besser, vor dem Entwurf eines komplexen Systemes darüber
nachzudenken, was digital Sinn macht und was man besser analog
realisiert. Mit analog sind eben auch SC-Filter gemeint. Ein
Hochschulprofessor, den ich selbst kenne, empfiehlt dies in einer
Vorlesung über digitale Filter seinen Studenten, wenn sie später
selbst komplexe elektronische Systeme entwickeln müssen.
Für den Studenten lohnt sich das Studium der SC-Technologie auch dann,
wenn es keine käuflichen SC-Filter-ICs mehr geben wird, weil in
Mikrominiaturschaltungen (IC-Design) - z.B. in Hörgeräten -
SC-Technologie sehr aktuell zum Einsatz kommt. Die SC-Technologie
beschränkt sich nicht bloss auf Filterfunktionen.
Links zu weiteren SC-Filter-Elektronik-Minikursen
- SC-Tiefpassfilter-Einheit mit umschaltbaren Grenzfrequenzen
- Steuerbares und steiles Tiefpassfilter in SC- und Analog-Technik und mit grossem Frequenzbereich
- 50-Hz-Notchfilterbank in SC-Filter-Technik (Teil 1)
- 50-Hz-Notchfilterbank in SC-Filter-Technik: PLL-Taktgenerator (Teil 2)
- Speziell: Sinusgeneratoren und der SC-Sinusgenerator