50-Hz-Notchfilterbank in SC-Filter-Technik (Teil 1)

Inhaltsverzeichnis

      1.   Einleitung

      2.   Das analoge 50-Hz-Notchfilter

      3.   Das SC-Notchfilter aus der Retorte

      4.   Welcher SC-Filter-Baustein kommt in Frage?

      5.   Lösung von Maxim

      6.   Das 50-Hz-SC-Notchfilter, die Schaltung

      7.   Diagramme

      8.   Die Erzeugung der Taktfrequenz

      9.   Der SC-Taktgenerator

    10.   Abgleich-Hinweis

    11.   Technische Daten

    12.   Links über SC-Filter



1.   Einleitung

Werden sehr kleine Wechselspannungen aus hochohmigen Signalquellen verstärkt, besteht meist das Problem, dass Störsignale mitverstärkt werden. Die meisten Störspannungen haben Gleichtakteigenschaften (Common-Mode). Sie sind asymmetrisch, d.h. sie treten zwischen Quelle und Erde auf. Daher ist es möglich solche Störungen weitgehend zu unterdrücken, wenn die Messung des Nutzsignales symmetrisch, vorzugsweise mit sogenannten Instrumentationsverstärkern erfolgt.

Die Gleichtaktstörspannung wirkt gleich stark auf beide Signalleiter die zum symmetrischen Eingang des Instrumentationsverstärker führen. Daher wird diese Störspannung theoretisch kompensiert. In der Praxis sieht es allerdings etwas schlechter aus, weil die Widerstände (Impedanzen) einer hochohmigen Quelle zwischen den beiden signalführenden Leitern und dem Signal-GND oft etwas unterschiedlich sind (Messung biologischer Signale mittels Elektroden (z.B. EMG) und dazu kommt, dass das E-Feld auch örtlich auf kleinem Raum nie ganz homogen ist. Es ist daher unvermeidlich, dass Reststörspannungen übrig bleiben, die mit geeigneten Massnahmen zusätzlich gefiltert werden müssen.

Mehr zum Thema symmetrische Spannungsmessung mit echten Differenzverstärkern (Instrumentationsverstärkern) liest man in den Elektronik-Minikursen Echter Differenzverstärker I, Echter Differenzverstärker II und Echter Differenzverstärker III, wobei auch gleich noch andere Themen rund um die Schaltung des Instrumentationsverstärkers, der schliesslich aus Operationsverstärkern (1) (2) besteht, behandelt werden.

Gewiss gibt es heute in der digitalen Signalverarbeitung (DSP) Möglichkeiten analoge Filtereigenschaften softwaremässig zu realisieren. Allerdings ist bei hoher Komplexität zu bedenken, dass es oft Sinn macht nicht unnötig Resourcen für Prozesse zu vergeuden, welche mit fixen Parametern arbeiten. Zudem ist es ohnehin oft besser, gleich zu Beginn das Problem an der Wurzel zu packen. Die in der Regel intensivste Gleichtaktstörung in einem Gebäude ist das 50-Hz-Wechselfeld der 230-VAC-Vernetzung. Es empfiehlt sich gleich nach der Vorverstärkung des Signales ein fixes, analoges Notchfilter (Kerbfilter) einzusetzen, um die restliche "Brummspannung" zu beseitigen.



2.   Das analoge 50-Hz-Notchfilter

Bild 1 zeigt ein fertig dimensioniertes Notchfilter aus einer "Applicationnote"-Sammlung von Texas Instruments. Ich habe hier allerdings die Widerstandswerte um einen Faktor 10 reduziert und die der Kapazitäten um den selben Faktor erhöht.

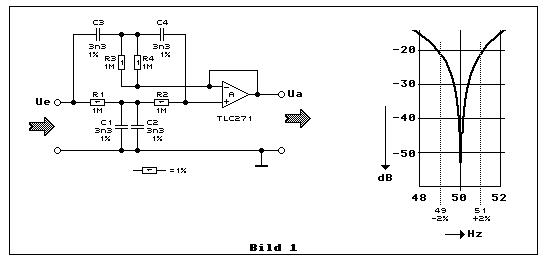
In der ursprünglichen Applicationnote hatten die Widerstände einen Wert von 10 M-Ohm. Damit wollte der IC-Hersteller vor Augen führen, wie extrem hochohmig die CMOS-Eingänge seiner LinCMOS-Operationsverstärker sind. So verständlich diese Werbung auch sein mag, empfehlenswert sind solch hohe Widerstandswerte an diesem Beispiel nicht.

Der geringste hygroskopische Effekt des Printschutzlackes oder die geringste Verschmutzung in den Zwischenräumen von Kontakten und Leiterbahnen reduzieren die Werte der sehr hochohmigen Widerstände mit dramatischer Auswirkung auf die Notchfrequenz. Selbst bei 1 M-Ohm ist eine absolut saubere Verarbeitung ein Gebot! Eine weitere Reduktion der Widerstände auf 100 k-Ohm beschert einem das Problem, dass einprozentige Kondensatoren mit einem Wert von 33 nF heute eher schwierig erhältlich sind und wenn doch, kaum preiswert und relativ gross sind.

Es gesellt sich ein weiteres Problem: Eigentlich müsste man Bauteiltoleranzen von einem Promille verwenden. Widerstände sind noch einigermassen erhältlich (jedoch sicher nicht preiswert). Kondensatoren hingegen kann man gleich vergessen - es ist sogar je länger desto problematischer, Kondensatoren mit 1%-Toleranzen zu finden.

Ein Abgleich mit Mehrgangpotentiometern ist durch die gegenseitige Beeinflussung von Resonanzfrequenz und Güte auch nicht gerade ein Kinderspiel. Für einen genauen Abgleich wird es also unumgänglich, weitere Widerstände oder Kondensatoren parallel zu schalten. Tut man dies nicht und die Gesamtoleranz weicht um gerade 2% ab, dann erkennen wir aus dem Diagramm in Bild 1, dass eine Dämpfung von >50 dB sich leicht auf 20 dB verschlechtert.

Bei all diesen Widerwertigkeiten stellt sich vor allem dann die Frage nach einer Alternative, wenn auf Grund von mehrkanaligen Anwendungen viele 50-Hz-Notchfilter zu realisieren und einzusetzen sind.



3.   Das SC-Notchfilter aus der Retorte

Das Prinzip einer solchen Alternative zeigt Bild 2. Bis vor bereits vielen Jahren gab es ein solches Notchfilter in SC-Technik. Es war der LMF90 von National-Semiconductor, der nicht mehr produziert wird. Die weitere Herstellung wurde auch nicht, wie viele andere Produkte, z.B. das universelle SC-Filter LMF100, von Texas-Instruments übernommen.

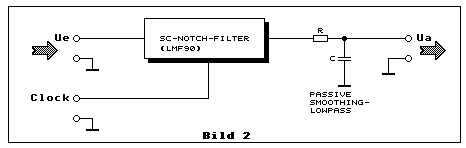
Die Notchfrequenz ergibt sich aus der Taktfrequenz dividiert durch die f_Clock/f_Notch-Ratio. Man musste am Ausgang des SC-Notchfilter bloss noch ein passives Tiefpassfilter zwecks Unterdrückung des Clockfeedthrouh beifügen und schon hätte man ein perfektes SC-Notchfilter. Dass die Produktion dieses scheinbar perfekt integrierten SC-Notchfilters eingestellt wurde, dürfte in den Nachteilen begründet sein. Wir betrachten dazu Bild 3 und lesen den folgendenText:

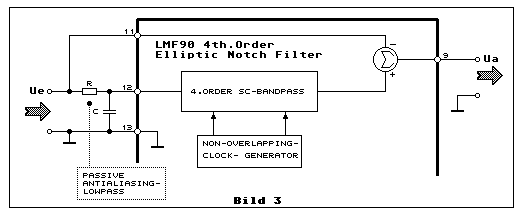
Bild 3 zeigt ein Teil des Innenleben des LMF90. Auf den Eingang an Pin 12 folgt ein SC-Bandpassfilter. Dessen Ausgang wird mit dem Eingangssignal an Pin 11 mit einem Summationsverstärker addiert. Daraus entsteht aus einem Bandpass- ein Bandsperr-, ein sogenanntes Notchfilter. Wunderbar!

Denken wir daran, dass ein SC-Filter stets ein abgetastetes System ist. Dieses hat einmal die Tücke des Abtasttheorems und, wie bei jedem SC-Filter, zusätzlich das Problem des Clockfeedthrough. Wird dieses SC-Notchfilter auf eine Notchfrequenz von 50 Hz dimensioniert und man wählt ein SC-Takt-/Notchfrequenz-Verhältnis von 100:1, dann beträgt das Verhältnis Abtastfrequenz zur Notchfrequenz noch 50:1. Wenn die Signalfrequenz grösser ist als die Hälfte der Abtastfrequenz, wird ein Aliaseffekt erzeugt. Dieser tritt allerdings erst in der Nähe der Abtastfrequenz in Erscheinung, weil es ein schmales Bandpassfilter ist, das IC-intern wirkt. Dies bedeutet, dass bei einer Signalfrequenz von 2450 Hz und 2550 Hz der erste Aliaseffekt auftritt. Für gewisse Anwendungen stört diese schmale Kerbe allerdings nicht. Um diesen Aliaseffekt zu vermeiden, müsste gemäss Datenblatt des LMF90 das passive Tiefpassfilter aus R und C vor den Eingang des SC-Bandpassfilters als Antialiasingtiefpassfilter geschaltet werden. Allerdings ist diesem passiven RC-Tiefpassfilter in Bezug auf Grenzfrequenz enge Grenzen gesetzt. Je niedriger die Grenzfrequenz gewählt wird, um so mehr sorgt die zusätzliche Phasenverschiebung zwischen den beiden Eingängen des Summationsverstärkers für eine Verschlechterung der Dämpfung bei der Notchfrequenz.

Betrachten wir aber noch das Problem des Clockfeedthrough. Diese Frequenz hat den Wert der Abtastfrequenz und nicht den der Taktfrequenz. Der Clockfeedthrough ist die Folge der Ladungsinjektion der IC-internen CMOS-Schalter und sie tritt im 10mV-Bereich am Ausgang Ua in Erscheinung. Nun kann man dieses Störsignal mit einer Frequenz von 2.5 kHz mit einem passiven oder aktiven Tiefpassfilter zusätzlich glätten, wie dies Bild 2 mit R und C zeigt. Damit hat man aber auf jedenfall eine geringere Nutzfrequenzbandbreite als die Abtastfrequenz zulässt. Selbst dann wenn es diesen integrierten Baustein noch gibt, muss man sich oft nach einer alternativ besseren Lösung umsehen, will man ein Notchfilter zur Unterdrückung der Netzfrequenz von 50Hz auf einer Signalleitung einsetzen, wenn man auch noch eine hohe Frequenzbandbreite benutzen will.



4.   Welcher SC-Filter-Baustein kommt in Frage?

Im Prinzip ist die Frage schnell beantwortet: Wenn man ein Tiefpassfilter bauen will, benötigt man ein integriertes SC-Tiefpassfilter-IC. Will man ein Notchfilter bauen, besorgt man sich eben ein integriertes SC-Notchfilter oder aber zumindest ein integriertes SC-Bandpassfilter. Mit einem zusätzlichen Opamp realisieren wir dann die Notchfunktion und wenn wir dabei nicht ein entsprechend hoher Aufwand mit Antialiasfilterung und Phasenkorrektur betreiben, haben wir die selben Probleme wie mit dem ausgestorbenen LMF90 von National-Semiconductor. Der zusätzliche Aufwand sorgt schnell für die Überlegung, ob es nicht einfacher wäre das SC-Notchfilter vollständig analog, nach alter Väter Sitte, zu realisieren. Wie auch immer, das heute modern gewordene oft extreme Bauklötzchendenken - zu jedem Problem ein fixfertiges IC - ist ausgeträumt bevor man richtig mit der Planung begonnen hat. Aber das ist in manchen ganz anderen schaltungstechnischen Problemen nicht viel anders. Der Elektronikneuling möge sich dies am besten gleich zu Beginn gut hinter die Ohren schreiben...

Die Firma Maxim bietet für die Realisierung der Notchfilterung eine grundlegende Applikation mit einem SC-Tiefpassfilter aus ihrer Produktepallette. Das IC hat die Bezeichnung MAX280. Es gibt auch einen MXL1062 mit der selben Funktionalität, ebenso vom Maxim. Dieser IC entspricht dem LTC1062 von Linear-Technology-Corporation (LTC).


  Drei Fliegen auf einen Schlag!

Das Besondere an diesem SC-Tiefpassfilter-IC ist, dass das Signal nicht durch den Filterbaustein hindurchfliesst. Das Signal wird bloss über einen Widerstand übertragen. Dieser Widerstand arbeitet mit dem SC-Filter als frequenzabhängiger Spannungsteiler, wodurch die Tiefpassfilterung zustande kommt. Damit schlägt man drei Fliegen auf einen Schlag: Die Filter-Schaltung erzeugt keine DC-Offsetspannung, dem Clockfeedthrough-Problem ist leicht beizukommen und es gibt keinen Aliaseffekt der durch die Verletzung des Abtasttheorems (Nyquist-Theorem) verursacht werden könnte. Dazu steht im Datenblatt folgender Satz: The input frequency range is not limited by the clock frequency because the MAX280/MXL1062 by itself does not alias. Dies gilt natürlich ebenso für den LTC1062 von LTC.

Man sollte sich jetzt von Maxim das Datenblatt "5th Order, Zero DC Error, Lowpass Filter MAX280/MXL1062" und von LTC das Datenblatt "LTC1062 5th Order Low Pass Filter" besorgen! Man sollte beide Datenblätter studieren, weil nicht beide den genau gleichen Inhalt haben.



5.   Lösung von Maxim

Figure 8b aus dem Datenblatt "5th Order, Zero DC Error, Lowpass Filter MAX280/MXL1062" von Maxim ist die Grundlage für die folgende Lösung. Diese Applicationnote ist in Bild 4 wiedergegeben:

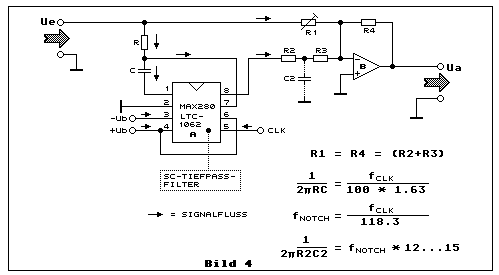
Wie wird aus einem Tiefpass- ein Bandsperrfilter (Notchfilter)? Beginnen wir bei einer sehr niedrigen Frequenz weit unterhalb der Grenzfrequenz des SC-Tiefpassfilter. Es darf auch eine DC-Spannung (0 Hz) sein. Die Spannung an Pin 7 des IC:A ist gleich gross wie die Eingangsspannung Ue, weil die Reaktanz des "Switched Capacitor Network" bei niedrigen Frequenzen so hochohmig ist, dass keine signifikante Spannungsteilung mir R in Serie erfolgt. C dient der DC-mässigen Entkopplung um DC-Offsetspannungen zu vermeiden. Auf Pin 7 folgt IC-intern ein Spannungsfolger mit niedriger Ausgangsimpedanz an Pin 8. Wenn R1 gleich gross ist wie R2 + R3, dann summieren sich beide Spannungen im Summationsverstärker B auf exakt den doppelten Wert am Ausgang Ua. Ua liegt um 6 dB höher als Ue.

Dies ist unsauber und weitgehend unbrauchbar! Es wird später gezeigt, wie dieses Problem behoben werden kann. Darauf lässt sich die Maxim-Applicationnote leider nicht ein. Diese Nachlässigkeit hat aber den Vorteil, dass man sich selbst etwas ausdenken muss und genau davon kann man als Schaltungsentwickler manchmal eine Menge lernen. Dies soll natürlich keine Aufforderung für Application-Ingenieure sein extra nachlässig zu arbeiten, und diese Haltung positiv als Dienstleistung zu erkennen. :-)

Betrachten wir jetzt, was passiert, wenn die Eingangsfrequenz erhöht wird. Die Phasenverschiebung zwischen Ue und Pin7 oder Pin 8 von IC:A nimmt zu und gleichzeitig fällt die Spannung an diesen beiden Pins auf Grund der Wirkung als Tiefpassfilter. Bei einer kritischen Frequenz an Ue wirken sich die Amplituden und die Phase so aus, dass am Ausgang des Summationsverstärker IC:B Ua die Spannung Null wird. Oberhalb dieser kritischen Frequenz steigt diese Spannung wieder an. Wir haben genau das was wir wollen, ein Notchfilter. Das Verhältnis zwischen der Takt- und der Notchfiltergrenzfrequenz hat hier einen "krummen" Zahlenwert von etwa 118. Um ein 50Hz-Notchfilter zu realisieren, muss man deshalb ebenso eine "krumme" Taktfrequenz erzeugen. Es sind etwa 5.9 kHz. Wie wir dieses Problem elegant lösen, sehen wir später. Es sei an dieser Stelle aber bereits erwähnt, dass sich der Aufwand nur für eine ganze Notchfilterbank - für den Einsatz einer mehrkanaligen Signalverarbeitungsanlage - und nicht für ein einzelnes Notchfilter lohnt.

Betrachten wir die Schaltung weiter und überlegen uns, was geschieht, wenn die Frequenz an Ue über die Notchfrequenz von 50 Hz hinaus erhöht wird. Die Amplitude am Ausgang des SC-Tiefpassfilters Pin 8 nimmt steil ab und nur wenig oberhalb der Grenzfrequenz des Tiefpassfilters wirkt sich diese Amplitude auf den Summationsverstärker IC:B kaum noch aus. Das passive Tiefpassfilter aus R2 und C2 unterdrückt das sogenannte Clockfeedthroughsignal.

Der grosse und sehr erwähnenswerte Vorteil des Schaltungsprinzipes dieses Maxim-SC-Tiefpassfilters ist die Tatsache, dass das Filter nur in einem sehr geringen Teil des Nutzfrequenzbereiches wirksam ist. Nämlich im schmalen Bereich seiner Grenzfrequenz (Cuttoff-Frequency). Im speziellen Fall eines Notchfilters muss allerdings noch das angedeutete 6-dB-Problem unterhalb der Notchfrequenz gelöst werden. Der Hauptpfad des Signales, ausserhalb der Filterwirkung, ist stets der direkte Weg zwischen Signaleingang Ue und dem (verstärkten/gepufferten) Ausgang Ua, wie auch alle andern Applikationen im Datenblatt zeigen. Diese Grundschaltung in Bild 4 steht Pate für die vollständige SC-Notchfilterschaltung in Bild 5 des folgenden Kapitels:



6.   Das 50-Hz-SC-Notchfilter, die Schaltung

Bild 5 zeigt die vollständige SC-Notchfilterschaltung:

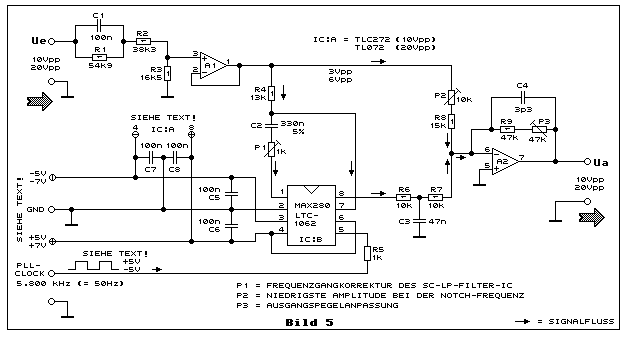
Sie besteht im Wesentlichen aus der Schaltung in Bild 4. Die wichtigste Erweiterung ist das passive Eingangs-RC-Netzwerk, bestehend aus C1, R1, R2 und R3. Dieses RC-Netzwerk unterdrückt die Spannungsüberhöhung bei einer Eingangsfrequenz unterhalb der Notchfrequenz bis zur DC-Spannung (0 Hz).

Betrachten wir vereinfacht zuerst den Fall, dass die Frequenz am Eingang von Ue oberhalb der Notchfrequenz liegt. C1 verhält sich wesentlich niederohmiger als der parallelgeschaltete R1. R1 ist durch C1 praktisch überbrückt. Es wirken daher einzig R2 und R3 als Spannungsteiler. Mit dieser Spannungsteilung wird die Aussteuerfähigkeit des SC-Tiefpassfilters IB:B dem Rest der Schaltung optimal angepasst. Der Klirrfaktor wird dadurch niedrig gehalten.

Ist man bereit, etwas mehr Klirrfaktor in Kauf zu zunehmen - wobei dies zu Gunsten eines besseren Signal-Rausch-Verhältnisses geht - kann man die Spannungsteilung des gesamten Eingangsnetzwerkes auch kleiner dimensionieren. Man erreicht aber nicht viel betreffs Verbesserung des Signal-Rausch-Verhältnisses, weil das Rauschen der gesamten Schaltung durch die Ausgangsrauschspannung des SC-Tiefpassfilter dominiert wird, obwohl diese Rauschspannung durch das passive Tiefpassfilter, bestehend aus R6 und C3, etwas gedämpft wird. Das SC-Filter als schwächstes Glied in einer analogen Schaltung in Bezug auf die Rauschspannung, gilt praktisch immer! Ob man trotzdem SC-Filter einsetzen kann, kommt auf die Anwendung an, wie z.B. bei der Digitalisierung auf die geforderte Auflösung der A/D- und/oder D/A-Wandler.

Der Summationsverstärker IC:A2 muss die Dämpfung des Eingangsnetzwerkes durch Verstärkung so kompensieren, damit die Gesamtverstärkung der Schaltung eins (0 dB) ist. Die Abstimmung dazu erfolgt mit dem Trimmpotentiometer P3. Die Dimensionierung des Eingangsnetzwerkes von IC:A1 bzw. der Ausgangsverstärkung von IC:A2, ist auch brauchbar, wenn andere Operationsverstärker, z.B. TL072 statt TLC272, mit ±12 VDC und damit mit entsprechend höherer Aussteuerbarkeit eingesetzt werden.

Die maximale Aussteuerbarkeit an Ue und Ua ist u.a. mit 10 Vpp angegeben. Für IC:A2 heisst dies allerdings, dass bei einer Betriebsspannung von ±5 VDC ein Opamp mit Rail-to-Rail-Ausgang verwendet werden muss oder man speist diesen Opamp mit einer höheren Spannung von z.B. ±7 VDC. Dies ist 2 VDC unter der empfohlenen maximalen Betriebsspannung der LinCMOS-Opamps von 16 VDC (± 8VDC), wie der TLC272 (Dual-Opamp) einer ist. Da die Worstcase-Betriebsspannung des SC-Filter-ICs MAX280, bzw. LTC1062, 18 VDC beträgt, kann IC:B ebenfalls auch mit ±7 VDC betrieben werden. Wünscht man sich eine Aussteuerung von maximal 20 Vpp, müsste der Opamp IC:A2 mit mindestens ±12 VDC, besser jedoch mit ±15 VDC, betrieben werden, wenn dieser, wie in Bild 5 angegeben, ein TL072 und somit kein Rail-to-Rail-Opamp ist. Das Dämpfungsnetzwerk R1, R2, R3, C1 und das Verstärkungsnetzwerk R9, P3 ist so dimensioniert, dass es für beide maximalen Aussgangsspannungen eingesetzt werden kann. Viele A/D- und D/A-Wandler-Schaltungen arbeiten im Bereich von 10 Vpp oder ±20 Vpp.

Betrachten wir, ebenso vereinfacht, jetzt den Fall, dass die Frequenz am Eingang von Ue unterhalb der Notchfrequenz liegt. In diesem Fall wäre gemäss Bild 4 und Maxim-Applicationnote die Ausgangsamplitude des SC-Tiefpassfilter-IC an Pin 7 gleich gross wie Ue. Die Folge davon wäre, dass die Amplitude an Ua doppelt so gross wäre. Genau dies verhindert das passive RC-Netzwerk am Eingang der Schaltung. Unterhalb der Notchfrequenz verhält sich C1 genügend hochohmig, so dass C1 auf das restliche Netzwerk keinen relevanten Einfluss hat. Es wirkt ebenso nur der Spannungsteiler, diesmal jedoch aus R1, R2 und R3.

Diese Spannungsteilung bewirkt, dass die Eingangsspannung an Ue doppelt so stark gedämpft wird, als wenn nur R2 und R3 wirken - dies zum Ausgleich, weil im Frequenzbereich unterhalb der Notchfrequenz der Summationsverstärker IC:A2 die Amplitude der Eingangsspannung, wie bereits beschrieben, verdoppeln würde. C1 spielt dabei das Zünglein an der Waage. Die Dimensionierung von C1 ist relativ unkritisch, wenn nicht gerade sehr hohe Präzision gefordert wird. Der Rippel beträgt im Übergangsbereich, knapp unter- und oberhalb der Notchfrequenz, bei der vorliegenden Dimensionierung etwa 1 dB. Es fällt daher kaum auf, weil diese Verzerrung schon nicht mehr im linearen Übertragungsbereich liegt.

Die Berechnung dieses RC-Netzwerkes dürfte sich in Abhängigkeit des SC-Tiefpassfilters recht schwierig gestalten. Ich schätzte den Wert von C1 grob und der Rest war empirisch. Die Funktion bleibt voll reproduzierbar, wenn man andere MAX280- oder LTC1062-Exemplare einsetzt.

P2 dient zum Abgleich für die niedrigste Amplitude bei der Notchfrequenz. R4 und C2 entsprechen der Funktion von R und C in Bild 4. Die Berechnungsformel ist dort angegeben. In der Applikationnote von Maxim fehlt aber ein Hinweis, dass es sogar möglich ist, in engen Grenzen die Notchfiltergrenzfrequenz ohne Taktfrequenzsteuerung zu beeinflussen. Ich entdeckte dies empirisch auf dem Testboard und die Funktion ist reproduzierbar wenn man MAX280- und LTC1062-Exemplare austauscht.

Dazu schaltet man ein Trimmpotmeter (P1) in Serie zu C2. Ohne diese einfache und ebenso elegante Möglichkeit würde die Realisierung einer SC-Notchfilterbank am schaltungstechnischen Aufwand scheitern. Das Verhältnis zwischen der Takt- zur Notchfiltergrenzfrequenz ist toleranzbehaftet. Gemäss Datenblatt des MAX280 (LTC1062) hat diese einen Wert von 100 mit einer Toleranz von ±1 Prozent. Diese Toleranz wirkt sich natürlich auch auf das "krumme" Verhältnis von f_Clock/f_Notch dieser Schaltung aus. Da man jedoch nicht für jedes Notchfilter eine separate Taktfrequenz realisieren möchte, ist die Abgleichsmöglichkeit mit P1 eine unbedingte Voraussetzung! Eine Abweichung von ±1 Prozent ist bei einem Notchfilter nicht vernachlässigbar. Kleiner Zusatzaufwand, grosse Wirkung, weil für diese zusätzliche Abstimmöglichkeit des Frequenzverhältnisses benötigt man nur gerade ein zusätzliches Trimmpotmeter und sonst nichts!



7.   Diagramme

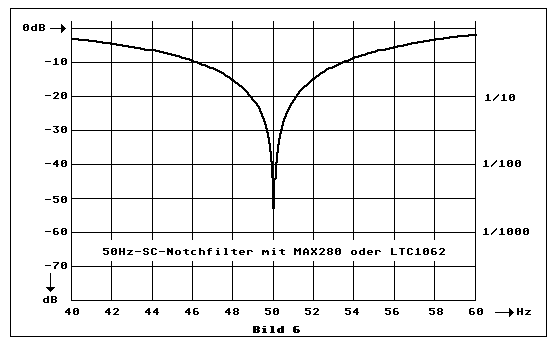
Bild 6 zeigt den Frequenzgang des SC-Notchfilters zwischen 40 und 60 Hz. Exakt abgestimmt ist dabei eine Amplitudendämpfung von mehr als 50 dB möglich. Dient die Schaltung zur Unterdrückung einer Spannung mit 50Hz-Netzfrequenz, welche sich z.B. in eine empfindliche Messanlage einkoppelt, dann macht es wenig Sinn, wenn die Amplitudendämpfung noch besser ist, weil die Netzfrequenz relativ oberwellenreich wurde. Wurde, weil dies vor allem durch den immensen Einsatz von Schaltreglern, vor allem in den vielen Computern, verursacht wird. Dies kommt durch das Nachladen der Elkos in der Nähe der Sinusscheitelwerte zustande. Diese Nachladung zieht kurzzeitig kräftige Ströme. Die Folge davon ist, dass die Scheitelwerte der Netzsinusspannung auf einem Oszilloskopen bereits gut sichtbare Verzerrungen zeigen. Diese erzeugen gewisse Oberwellenanteile hauptsächlich bei 150 Hz, 250 Hz, usw., die ebenfalls, meist kapazitiv, in die Messsysteme mit eingekoppelt werden.

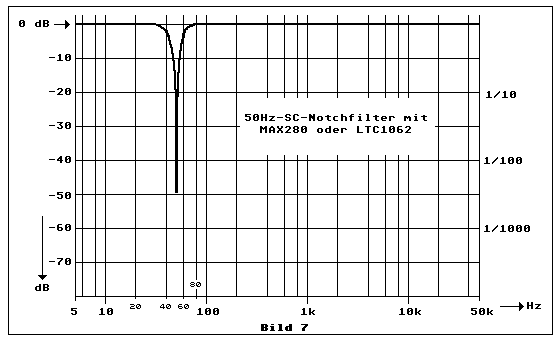
Bild 7 zeigt den Frequenzgang des SC-Notchfilters innerhalb einer Frequenzbandbreite von 50 kHz in logarithmischer Frequenz-Skalierung. Man bedenke dabei, dass das SC-Filter nur gerade in der Region unterhalb und bis zur Notchfrequenz beteiligt ist. Oberhalb wirkt einzig die Übertragung über P2 und R8 (Bild 5).



8.   Die Erzeugung der Taktfrequenz

Gemäss Formel in Bild 4 ergibt sich eine Taktfrequenz von 5915 Hz. Dies stimmt allerdings nur für diese aus dem MAX280-Datenblatt kopierte Applicationnote. Wird in Bild 5 das passive R4C2-Tiefpassfilter und die Abgleichmöglichkeit mit P1 angewendet, verschiebt sich das Verhältnis f_Clock/f_Notch etwas. Der optimale Wert liegt bei 116 statt bei 118.3, was einer Taktfrequenz von 5.8 kHz entspricht.

Es stellt sich hier die Frage, wie man am besten und mit geringstem Aufwand eine präzise Taktfrequenz erzeugt. Es stellt sich aber ebenso die Frage, was eine hohe Frequenzstabilität überhaupt bringt, weil die Netzfrequenz geringen, wenn auch sehr kurzzeitigen Schwankungen unterworfen ist. Die Erzeugung einer quarzstabilen Frequenz, bei der man ohne PLL-Frequenz-Multiplier hier nicht auskommen würde, ergibt einen gewissen Aufwand, bei dem man sich sogleich fragen kann: Warum denn diese PLL-Schaltung nicht gleich mit der Netzfrequenz synchronisieren? Der Vorteil liegt auf der Hand, weil dadurch die Notchfrequenz automatisch einer Änderung der Netzfrequenz angepasst wird. Dies funktioniert allerdings nur in schmalen Grenzen, wenn man ein SC-Tiefpassfilter zu einem SC-Notchfilter umbaut. Es bringt hier allerdings eine eindeutige Verbesserung: Bei einer Abweichung der Sinusfrequenz an Ue (Bild 5) zwischen 49Hz und 51 Hz (±2 %) ist die Amplitudendämpfung bei der Notchfrequenz um 8 dB besser, wenn sich die Takt- bzw. Notchfrequenz um dieselbe prozentuale Abweichung anpasst. Die tatsächliche kurzzeitige Abweichung von der Sollnetzfrequenz ist bei der heutigen Vernetzung der elektrischen Kraftwerke wesentlich geringer. Dies ist jedoch nicht der Fall, wenn die Schaltung in einem Gerät zur Anwendung kommt, wo die Netzspannung aus einem einzelnen (Diesel-)Generator erfolgt.



9.   Der SC-Taktgenerator

Diese Schaltung und die Beschreibung dazu folgt in einem zweiten Teil. Dazu gibt es zwei Gründe: Dieser Elektronik-Minikurs wird nicht zu gross und die Syntheziserschaltung kann auch für ganz andere Anwendungen mit andern Parametern eingesetzt werden kann. Die Fortsetzung liest man in:




10.   Abgleich-Hinweis 

 
1. P1 auf Notchfrequenz trimmen.

2. P2 auf niedrigste Amplitude an
Ua bei Notchfrequenz trimmen.

3. Punkt 1 und Punkt 2 evt. nachtrimmen.

4. P3 so einstellen, dass die Verstärkung
im Durchlassbereich 0 dB beträgt.


11.   Technische Daten 

 
Maximale Eingangsspannung an Ue:        10 Vpp  (20 Vpp)

Maximale Ausgangsspannung an Ua:        10 Vpp  (20 Vpp)

Verstärkung im Durchlassbereich:         0 dB

Dämpfung bei der Notchfrequenz:         50 dB

Notchfrequenz:                          50 Hz

Notchfrequenzbandbreite (-3dB):         ± 10 Hz

Dämpfungsverbesserung durch PLL:        8 dB  (49 Hz - 51 Hz)

Frequenzbandbreite total:               DC - 100 kHz

Signal-/Rauschverhältnis:               85 - 90 dB

Eingangs-Widerstand:                    55 k-Ohm  (f > 50 Hz)
110 k-Ohm  (f < 50 Hz)

Betriebsspannung:                       siehe Text!

Betriebsstrom pro Filterschaltung:      ca. ± 6 mA


12.   Links