Sinusgeneratoren und der SC-Sinusgenerator
Einleitung
Es gibt unterschiedliche Methoden eine Sinusspannung zu erzeugen. Für
hohe Frequenzen verwendet man gerne LC-Oszillatoren, während man bei
niedrigeren Frequenzen RC-Oszillatoren, wie z.B. einen
Phasenschieber-Oszillator, einsetzt. Besonders erwähnenswert ist der
Wien-Robinson-Oszillator. Bei guter Dimensionierung erreicht man sehr
niedrige Klirrfaktorwerte und eine gute Frequenzstabilität. Dies
erreicht man dadurch, dass im Resonanzfall die Verstärkung die Dämpfung
des frequenzselektiven Netzwerkes im Rückkopplungspfad mittels Regelung
gerade so kompensiert, dass eine bestimmte Sinusspannung konstant
gehalten wird. Eine derart erzeugte Sinusspannung hat wie ein
LC-Oszillator etwas Natürliches an sich, weil die Sinusform durch ein
Resonanzphänomen erzeugt wird.
Im ersten Kapitel widmen wir uns ein wenig diesem Generatortyp mit einer
erprobten Schaltung, die man leicht den eigenen Bedürfnissen anpassen
kann. Man lernt dabei auch eine Art der Verstärkerregelung mittels JFET
kennen, wie man sie auch gerne bei Dynamikkompressoren einsetzt. In den
weiteren Kapiteln wird in groben Zügen mittels Blockschemata gezeigt,
wie der Funktionsgenerator und der Frequenzsynthesizer arbeiten. Mit
Schieberegistern und einem Widerstandsnetzwerk an den parallelen
Datenausgängen lässt sich jede Spannungsfunktion, und damit auch eine
Sinusspannung, erzeugen. Die Frequenz der Sinusspannung ist ebenso mit
einer Taktfrequenz steuerbar. Diese Methode eignete sich bereits in den
frühen 1970er-Jahren hervorragend für die FSK-Modulation (FSK =
Frequency-Shift-Keying). Da diese Art der Sinuserzeugung aufwändig ist,
wird sie heute nicht mehr realisiert. Trotzdem lohnt es sich zu lernen,
wie so etwas funktioniert. Es kann eine Anregung für andere Projekte mit
Schieberegistern sein. Es gibt längst Alternativen, wie ein relativ
einfacher digitaler Sinusgenerator mittels (E)EPROM und die sogenannte
DDS-Methode. Diese beiden Methoden werden kurz vorgestellt.
Damit stecken wir bereits in der Thematik der digital erzeugten
Sinusspannung. Wir setzen das Thema mit dem Titel "Aus Rechteck wird
Sinus", mit einer spektralen Betrachtung der zeitsymmetrischen
Rechteckspannung praxisnah fort. Es wird gezeigt, dass mit geeigneter
Tiefpassfilterung aus einer solchen Rechteckspannung eine brauchbare
Sinusspannung erzeugt wird. Dass aus all dem dieser Elektronik-Minikurs
auf einen Sinusgenerator mittels SC-Tiefpassfilter hinausläuft, dessen
Sinusfrequenz ganz leicht mit einer frequenzvariablen Rechteckspannung
steuerbar ist, ist dann bloss noch die logische Konsequenz. Es gibt dazu
eine praxiserprobte Schaltung.
Der Wien-Robinson-Oszillator
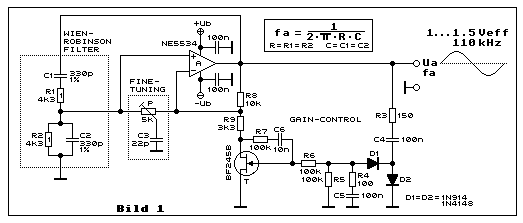
Bild 1 zeigt einen typischen Wien-Robinson-Oszillator, ein Teil aus
einem meiner früheren Projekte. Als Opamp kommt ein NE5534 zum Einsatz.
Es kann auch ein anderer Opamp sein, der etwa das selbe
Gain-Bandbreite-Produkt von 10 MHz und eine Slewrate von etwa 13 V/µs
aufweist. Dies trägt wesentlich zu einem niedrigen Klirrfaktor bei, denn
die Frequenz der Sinusspannung liegt im unteren 100-kHz-Bereich. Da der
Opamp mit niedriger Verstärkung arbeitet, sollte dieser
"unity-gain-stable" sein oder zumindest die Möglichkeit eines
zusätzlich externen Ableichs der Frequenzgangkompensation mit einem
Kondensator haben.
Das Wien-Robinson-Filter aus R1, C1, R2 und C2 hat eine Resonanzfrequenz
von 110 kHz. Wenn die Schaltung in Betrieb gesetzt wird, beginnt sofort
das Oszillieren. Die Sinusspannung Ua steigt schnell und würde ohne
automatische Verstärkungsregelung durch die Betriebsspannung von ±Ub
begrenzt. Genau genommen, ist die Amplitude der begrenzten Sinusspannung
etwas niedriger, weil der verwendete Opamp am Ausgang nicht
rail-to-rail-fähig ist.
Die Detailschaltung GAIN-CONTROL reduziert bei einer bestimmten
Sinusspannung Ua die Verstärkung des Oszillators, damit das Oszillieren
gerade soweit aufrecht erhalten wird, dass sich eine konstante
Sinusspannung einstellt. Diese Verstärkung liegt bei etwa 3. Es ist
wichtig, dass man die Regelschaltung nicht überfordert, damit diese
nicht selbst instabil wird. Man sollte daher die maximale ungeregelte
Verstärkung nicht zu hoch dimensionieren. Die maximale Verstärkung
ergibt sich aus R8 und R9 mit einem Wert von etwa 4.
RDS-ON des JFET T bleibt hierbei unberücksichtigt.
RDS-ON ist dann minimal, wenn das Gate des JFET auf
Sourcepotential liegt. Dies trifft dann zu, wenn nach dem Einschalten
noch keine Sinus- oder nur eine sehr kleine Sinusspannung vorliegt. Bei
ansteigender Sinusspannung beginnt der gleichrichtende
Spannungsverdoppler, bestehend aus C4, D1, D2, R4 und C5, zu arbeiten.
Die negative Gatespannung am JFET T steigt und
RDS-ON steigt bis die Verstärkung soweit reduziert
ist und sich eine konstante Sinusspannung an Ua einstellt. R5 und C5,
welche die Gatespannung liefern, bilden eine Zeitkonstante, die um
Grössenordnungen grösser sein muss, als die Periode der Sinusspannung.
Je grösser diese Zeitkonstante ist, um so rippelfreier ist die
Gatespannung und um so niedriger ist der Klirrfaktor der Sinusspannung.
Bei zu grosser R5C5-Zeitkonstante ist die Einschwingdauer unerträglich
lang, dies aber hauptsächlich bei niederfrequenter Sinusspannung. R6, R7
und C6 dienen der Linearisierung des JFET. R6 und R7 sind in der Praxis
etwa gleich gross. Ersetzt man R7 durch ein vielgängiges Trimmpotmeter,
kann man den Klirrfaktor besonders niedrig einstellen. Die
JFET-Linearisierung wird dadurch erreicht, dass ein Teil der
veränderlichen Drain-Source-Spannung zur Gate-Source-Spannung addiert
wird. C6 dient nur dazu, dass kein DC-Strom von Drain in Richtung R6
abfliesst. R3 und R4 dienen dazu, dass die Regelschaltung etwas
gedämpft wird und so nicht selbst zum sehr niederfrequenten Schwingen
(Pumpen) neigt. Eine Spannungsverdopplung hat gegenüber einer einfachen
Gleichrichtung den Vorteil, dass auch niedrige Sinusspannungen geregelt
werden können.
Dieser Wien-Robinson-Oszillator, auch Wien-Brücken-Oszillator genannt,
kann man natürlich auch für ganz andere Frequenzen einsetzen. Dazu
müssen die Bauteile des Wien-Robinsohn-Filter (siehe Formel) und -
falls überhaupt erwüscht - das FINE-TUNING angepasst werden. Bei
niedrigerenn Sinusfrequenzen müssen die Komponenten des GAIN-CONTROLL
ebenfalls angepasst werden (höhere R5C5-Zeitkonstante). Vor einem
definitiven Schaltungsentwurf ist die Experimentierfreude mit einem
Testboard empfohlen.
Im berühmten Buch Halbleiter-Schaltungstechnik von U. Tietze und
Ch. Schenk ist der Wien-Robinson-Oszillator ausführlich beschrieben.
Der Funktionsgenerator

Bild 2 zeigt blockschematisch einen sogenannten Funktionsgenerator. Die
positive Eingangsspannung Ue steuert über den elektronischen analogen
Schalter (Analog-Switch) einen aktiven mit Opamp realisierten
invertierenden Intergrator. Dessen Ausgangsspannung sinkt linear und sie
steuert den Schmitt-Trigger. Dieser schaltet bei einer unteren
Schaltschwelle um und weil dieses Signal den analogen Schalter steuert,
wird der Eingang Ue beim Integrator von einer Teilspannung von +Ub auf
GND geschaltet. Dadurch steigt die Integratorspannung, ebenso linear,
bis zu einer oberen Schaltschwelle des Schmitt-Triggers und der ganze
Vorgang beginnt von Neuem. Am Ausgang des Schmitt-Triggers Uar
(r = Rechteck) zeigt sich eine Rechteck- und am Ausgang des Integrators
Ud (d = Dreieck) eine Dreieckspannung. Wie man einen solchen
Dreieckgenerator mit wenig Aufwand selbst realisieren kann, zeigt der
Elektronik-Minikurs (5). Ein
Dreieck-Sinus-Converter, das meist aus einem komplexen
Widerstands-Dioden-Netzwerk besteht, erzeugt aus dem Dreiecksignal ein
"künstliches" Sinussignal Uas (s = Sinus).
Ich bezeichne diese Methode der Sinuserzeugung "künstlich", weil die
Sinusspannung nicht aus einem Resonanzkreis angeregt, sondern
elektronisch mittels Approximation erzeugt wird. Mit der Variation von
Ue, z.B. mittels Potmeter P, kann man die synchrone Frequenz der drei
Signale Rechteck, Dreieck und Sinus steuern. Wichtig um einen möglichst
niedrigen Klirrfaktor zu erzeugen, ist es, dass die Rechteckspannung
möglichst zeitsymmetrisch, also mit einem Tastverhältnis von 0.5
erfolgt. Dies stellt vor allem Ansprüche an die Dimensionierung der
Umschaltpegel des Schmitt-Triggers. Ein sehr berühmter,
traditionsreicher und noch heute empfehlenswerte Vertreter eines solchen
Funktionsgenerator-IC, für niedrige bis mittlere Frequenzen bis knapp 1
MHz, ist der XR2206 von Exar. Will man einen "sauberen" Sinus, sollte
man nicht wesentlich über 100 kHz hinausgehen.
Frequenzsynthesizer (Frequenzmultiplier)
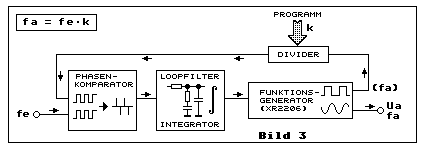
Bild 3 bindet einen Funktionsgenerator, wie Bild 2 zeigt, in ein
Phase-Locked-Loop-System (PLL-System) ein. Die Frequenzen an den beiden
Ausgängen Sinus (Ua, fa) und Rechteck (fa) des Funktionsgenerators sind
identisch. Die Frequenz fa wird mittels programmierbaren Frequenzteiler
durch den Wert k geteilt und gelangt zum einen Eingang des
Phasenkomparators. Der andere Eingang wird von der Eingangsfrequenz fe
gesteuert. Der Phasenkomparator vergleicht die Phasen und damit auch die
Frequenzen seiner beiden Eingänge. Auf den Ausgang des Phasenkomparators
folgt ein Integrator, das sogenannte Schlaufen-Tiefpassfilter
(Loop-Lowpass). Dieses integriert die Impulse zur Steuerspannung für
den VCO - Teil des des Funktionsgenerators. Im eingeschwungenen Zustand
stellt sich eine Sinusfrequenz fa ein, die der Eingangsfrequenz fe,
multipliziert mit dem Teilerfaktor k, entspricht. Dies muss so sein,
weil die beiden Eingänge des Phasenkomparator phasenidentisch und damit
auch frequenzidentisch sein müssen. Dies allerdings nur dann, wenn der
Phasendiskriminator nicht auch auf das ganzzahlige Vielfache der
Frequenz fe einrastet. Eine gewöhnliche EXOR-Schaltung eignet sich daher
nur beschränkt als Phasenkomparator.
Man kann eine solche PLL-Schaltung auf zwei Arten einsetzen. Entweder
als Frequenzsynthesizer, bei dem fe eine quarzstabile Referenzfrequenz
ist und die Ausgangsfrequenz fa mit dem Frequenzteiler programmierbar
ist. Oder die Frequenzteilung k ist fix und die PLL-Schaltung arbeitet
als Frequenzmultiplier fa=fe*k. Ein solches Beispiel bietet der
Elektronik-Minikurs (4).
Sinusgenerator mit Schieberegister
Diese Methode ist zwar längst Geschichte. Es ist aber trotzdem interessant zu verstehen wie so etwas funktioniert. Man weiss auch nie, ob dieses Funktionsprinzip, in abwandelter Form, nicht irgendwann trotzdem nützlich sein kann. Diese Methode war in den 1970er- bis weit in die 1980er-Jahre sehr selbstverständlich. Man kann ein Sinussignal aus einem höherfrequenten Taktsignal (Clocksignal) mittels Schieberregister mit einem seriellen Dateneingang, einer Anzahl paralleler Datenausgänge, einem Widerstandsnetzwerk und einer Opampschaltung erzeugen, wie dies Bild 4 illustriert:
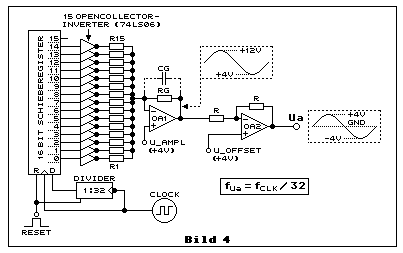
Bild 4 zeigt die Prinzipschaltung. Ein Frequenzteiler DIVIDER
teilt die Taktfrequenz durch die Anzahl Schieberegister-Takte pro
Sinusperiode und sorgt dafür, dass während 16 Takten logische HIGH- und
während ebenfalls 16 Takten logische LOW-Pegel durch das Schieberegister
an die parallelen Datenausgänge geschaltet werden. Diese Ausgänge füllen
sich also mit HIGH-, danach mit LOW-Pegeln und dann beginnt das Ganze
von Neuem. Beim Starten muss ein Resetimpuls zuerst Schieberegister und
Teiler auf Null setzen, wobei während dieser kurzen Phase kein
Taktsignal das Schieberegister und den Frequenzteiler erreichen darf.
Die Schaltung mit Opamp OA1 arbeitet als digital gesteuerter
Verstärker. Die Sinusfunktion ergibt sich durch die Dimensionierung der
Widerstände R1 bis R15. Die treppenförmige Sinusspannung kommt dadurch zustande,
dass durch das schrittweise Hinzuschalten der Widerstände R1 bis R15,
die Ausgangsspannung von OA1 von +4 V bis +12 V schrittweise erhöht und
anschliessend durch das schrittweise Ausschalten dieser Widerstände
wieder von +12 V auf +4 V reduziert wird. Die Verstärkung von OA1
ändert sich schrittweise von 1 nach 3 und danach wieder zurück. Die
Amplitude der Sinusspannung wird durch die Spannung
UAMPL (AMPL = Amplitude) definiert. Die
DC-Offetspannung wird davon ebenfalls beeinflusst.
+4 V am Ausgang von OA1 liegt dann vor, wenn alle Widerstände (R1 bis
R15) ausgeschaltet sind, weil dann arbeitet OA1 mit maximaler
Gegenkopplung durch RG mit Verstärkung 1. OA1 muss daher
unity-gain-stable sein! Das Ein- und Ausschalten dieser Widerstände
besorgen die Open-Collector-NPN-Transistoren an den Ausgängen der
einzelnen Inverter der drei ICs 74LS06. Dass nur 15 Datenausgänge des
Schieberegisters benutzt werden kommt daher, dass der inaktive Zustand
aller 15 Ausgänge auch gilt. Es sind also total 16 Zustände pro
Halbperiode.
Wozu braucht es OA2? OA1 kann nur eine treppenförmige Sinusspannung im
positiven Spannungsbereich liefern. OA2 kompensiert mit
UOFFSET diese DC-Offsetspannung, so dass an Ua die
Sinusspannung amplitudensymmetrisch um den GND-Pegel liegt.
CG und RG wirken als einfaches
passives Tiefpassfilter, das die Stufenform glättet. Diese sehr einfache
Filterung genügt aber nur bei quasistationärer Sinusfrequenz.
CG und RG bilden alleine die
Grenzfrequenz. Wegen der niedrigstohmigen virtuellen Spannung am
nichtinvertierenden Eingang von OA1, haben R1 bis R15 keinen Einfluss
auf diese Filterung. Für viele Anwendungen braucht es jedoch diese
Filterung gar nicht.
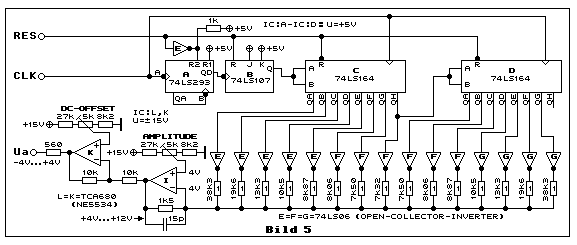
Diese fertig dimensionierte Schaltung war Teil einer Arbeit von mir aus dem Jahre 1974, bei der es darum ging einen digital gesteuerten FSK-Sender zu bauen. Wer wissen möchte was FSK bedeutet, möge sich mit einer Suchmaschine (Yahoo, Google, etc.) schlau machen. Diese Schaltung ist mit dem Text zu Bild 4 bereits ausführlich erklärt. Deshalb folgen bloss noch einige Ergänzungen. IC:A (74LS293) ist ein asynchroner 4-Bit-Counter, der die Aufgabe hat das Taktsignal CLK durch 16 zu teilen. Da es einen Frequenzteiler braucht, der gesamthaft durch 32 teilt, wurde mit IC:B (74LS107) ein JK-Flipflop nachgeschaltet. IC:C und IC:D sind je ein 8-Bit-Serie-Parallel-Schieberegister (74LS164). Für die Open-Collector-Inverter wurden mit IC:E bis IC:G drei ICs des Typs 74LS06 benötigt. Eines der Inverter wird für den Reset beim IC:A benötigt. Der Widerstand von 1 k-Ohm ist nötig, um beim Reset-Eingang ein HIGH-Pegel zu erzeugen, weil dies ein Open-Collector-Inverter nicht liefern kann.
Digitaler Sinusgenerator mit (E)EPROM
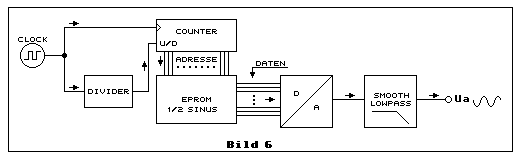
Anstelle der beiden Schieberegister mit den sehr vielen
Präzisionswiderständen, geht es auch mit einem (E)EPROM. Um ein
Sinussignal zu erzeugen, wird im vorliegenden Beispiel eine halbe
Sinusperiode numerisch als Tabelle gespeichert. Ein Zähler schaltet das
E(EPROM) von Adresse zu Adresse und diese senden die Daten der
Sinustabelle Schritt für Schritt zum D/A-Wandler. Am Ausgang des
D/A-Wandler bildet sich eine treppenartige Sinusspannung, dessen Stufen
mittels Tiefpassfilter (Smooth-Lowpass) geglättet werden, falls dies
nötig ist. Bei grosser Frequenzvariation muss die Grenzfrequenz des
analogen Tiefpassfilters variabel mit der Sinus- bzw. Taktfrequenz
synschronisiert sein. Dazu eignet z.B. ein Frequenz/Spannungs-Wandler
und ein OTA in der Funktion als spannungssteuerbares
zeitkontinuierliches aktives Tiefpassfilter. Dieses OTA-Thema ist u.a.
in (3) thematisiert.
Diese (E)EPROM-Methode erlaubt jede andere Kurvenform numerisch zu
speichern. Man bezeichnet einen solchen Generator daher auch als
Arbitrary-Function-Generator, auf deutsch: Ein Generator mit
willkürlicher Kurve...
Die Direkte Digital Synthese (DDS)
Die zur Zeit (2007) modernste Methode der Sinuserzeugung ist die sogenannte Direkte Digital Synthese (DDS). Damit lassen sich bis zu hohen Frequenzen klirr- und rauscharme Sinussignale erzeugen. Wenn sich jemand dafür interessiert, dem bietet die Suche im Internet reichhaltige Information an. Ein breites Spektrum an DDS-Schaltkreisen findet man bei Analog-Devices. ELV bietet einen Bausatz für ein DDS-Board mit einer LCD-Anzeige und Frequenzeinstellung mittels Inkremetalgeber und Taster.
Aus Rechteck wird Sinus
Uns interessiert hier eine ganz andere Methode und dies erst noch mit wenig materiellem Aufwand. Zunächst geht es um die Frage, wie man aus einem absolut zeitsymmetrischen Rechtecksignal (Tastverhältnis t/T = 0.5) ein klirrfaktorarmes Sinussignal erzeugt. Wie befassen und zuerst etwas mit dem Frequenzspektrum eines solchen Rechtecksignales und beginnen mit Bild 7:
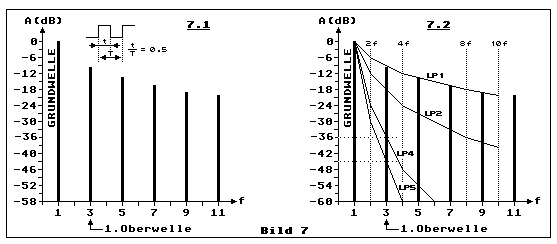
Teilbild 7.1 zeigt das Frequenzspektrum eines zeitsymmetrischen
Rechtecksignales (t/T = 0.5). Dieses besteht aus der Frequenz der
Grundwelle und aus den Frequenzen der ungeradzahligen Oberwellen. Diese
treten mit zunehmender Dämpfung bei der 3-fachen (1. Oberwelle), bei der
5-fachen (2. Oberwelle), bei der 7-fachen (3. Oberwelle), bei der
9-fachen (4. Oberwelle), bei der 11-fachen (5. Oberwelle) Grundfrequenz
u.s.w. auf. Diese Reihe kann theoretisch unendlich fortgesetzt werden.
Bei einer theoretisch unendlich hohen Flankensteilheit des
Rechtecksignales, ist dieses Frequenzspektrum, mit seinen diskreten
Frequenzen, ebenfalls unendlich lang. Darum ist es auch möglich mit
einem sehr steilflankigen Rechtsignal, mit einer niedrigen Frequenz von
z.B. nur 1 kHz, die Radiobänder von der Langwelle bis in den UKW-Bereich
zu stören. Dies nur am Rande erwähnt.
Teilbild 7.2 zeigt das selbe Diagramm noch einmal. Diesmal jedoch mit
den Dämpfungskurven von Tiefpassfiltern, dessen Grenzfrequenz auf die
Frequenz der Grundwelle des Rechtecksignales dimensioniert ist. Es gilt
die Regel, dass ein Tiefpassfilter das Signal oberhalb seiner
Grenzfrequenz um 6 dB pro Frequenz-Oktave pro Ordnungszahl dämpft.
Diese Steilheit beobachtet man allerdings beim Überschreiten der
Grenzfrequenz noch nicht. Das was an diesem Punkt geschieht, ist
abhängig von der sogenannten Filtergüte, die uns hier nicht weiter
interessiert. LP1 (LP = Low-Pass) ist die Dämpfungskurve eines
Tiefpassfilters 1. Ordnung, mit 6 dB/Oktave (Oktave = doppelte Frequenz)
oder 20 dB/Dekade. Man beachte die Kurve LP1 bei den punktierten
senkrechten Linien bei 2f und 10f. LP2 zeigt bei 2f eine Dämpfung von 12
dB und bei 10f 40 dB. LP4 zeigt bei 2f eine Dämpfung von 24 dB und bei
10f 80 dB (nicht mehr gezeichnet). LP5 zeigt bei 2f eine Dämpfung von 30
dB und bei 10f 100 dB (nicht mehr gezeichnet). Weshalb die Kurve eines
Tiefpassfilters 5. Ordnung eingezeichet ist, wird weiter unten
thematisiert. Weshalb alle Filterkurven nicht linear im Diagramm
erscheinen, kommt daher, weil die dB-Skala logarithmisch, die
Frequenz-Skala jedoch linear dargestellt ist.
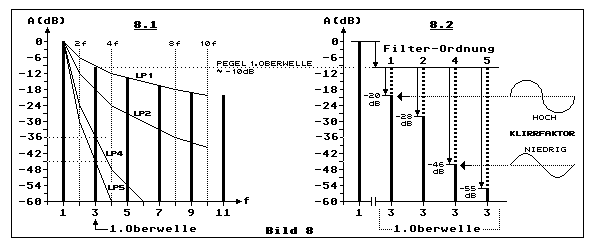
Teilbild 8.1 wiederholt Teilbild 7.2 und diesem Diagramm steht das von
Teilbild 8.2 zum Vergleich gegenüber. Die Dämpfungskurven der
Tiefpassfilter LP1 bis LP5 in Teilbild 8.1 sind nur dann exakt, wenn das
Signal am Eingang von LP1 bis LP5 Sinusspannungen sind.
Beispiel: Wir verwenden ein Tiefpassfilter 4. Ordnung, also LP4. Die
Grenzfrequenz von LP4 ist identisch mit der Grundfrequenz im Diagramm.
Die Frequenz der Sinusspannung am Eingang von LP4 entspricht der ersten
Oberwelle, also der dreifachen Grenzfrequenz von LP4. Die Dämpfung der
Sinusspannung am Ausgang von LP4 beträgt 36dB. Beachte die Kurve von LP4
beim Kreuzen mit der ersten Oberwelle. Die Amplitude der ersten
Oberwelle (dies ist eine Sinusspannung) des zeitsymmetrischen
Rechtecksignales hat aber nicht eine Relativspannung von 0 dB, sondern
etwa -10 dB. Dieser Dämpfungswert muss zur Filterdämpfung bei der
3-fachen Grenzfrequenz dazu addiert werden. Daraus entsteht eine
Gesamtdämpfung von 46 dB, wie dies Filter-Ordnung 4 (LP4) in Teilbild
8.2 zeigt.
Voraussetzung für diese Addition ist natürlich, dass
Filtergrenzfrequenz und Signalgrundfrequenz identisch sind. Aus
praktischen Überlegungen ist es allerdings oft besser, wenn die
Filtergrenzfrequenz etwas höher ist als die Signalgrundfrequenz, weil
bei Frequenzvariation der Rechteckspannung die Amplitudenstabilität der
Sinusspannung am Ausgang des frequenzsteuerten SC-Tiefpassfilters besser
gewährleistet ist. Das werden wir an einer praktischen Anwendung noch
sehen.
Teilbild 8.2 zeigt eine Zusammenstellung der Dämpfungswerte für die
erste Oberwelle für die Filterordnungen 1 bis 5. Höhere Oberwellen sind
nicht relevant, da die Dämpfungswerte noch höher sind. Beim
Tiefpassfilter 5. Ordnung beträgt die Dämpfung 55 dB. Wenn ein
Klirrfaktor von etwa 0.5 % bis 1% ausreicht, genügt eine Dämpfung 46
dB. Also eignet sich ein Tiefpassfilter 4. Ordnung. Allerdings mit dem
Vorbehalt, dass die Grenzfrequenz mit der Signalgrundfrequenz identisch
ist. Soll die Grenzfrequenz etwas höher sein, ist ein Tiefpassfilter 5.
Ordnung geeigneter.
Sinus aus Rechteck mit fixer Frequenz
Bevor wir uns mit dem SC-Tiefpassfilter befassen, wollen wir zunächst feststellen, was es bringt, anstelle eines Wien-Robinson-Oszillators (Bild 1) ein Rechteckgenerator und ein Butterworth-Tiefpassfilter 5. Ordnung zu verwenden, um eine Sinusspannung zu erzeugen, wie dies Bild 9 illustriert und dies unter der Voraussetzung, dass die Signalfrequenz konstant ist. Man betrachte Bild 9:
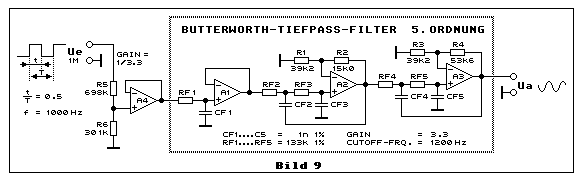
Wenn man beide Schaltungen von Bild 1 und Bild 9 vergleicht ist, ist Bild 9 eher aufwändiger, denn die Schaltung des notwendigen Rechteckgenerators ist in Bild 9 nicht enthalten. Ein Fine-Tuning der Frequenz ist in beiden Schaltungen möglich. Will man jedoch eine hochpräzise fixe Sinusfrequenz, eignet sich Bild 9 besser, weil ein quarzstabiler Rechteckgenerator diese Forderung leicht erfüllt. Die Schaltung in Bild 9 ist dann eindeutig überlegen, wenn man verschiedene Sinusfrequenzen benötigt, die zu einander ein präzises Frequenzverhältnis haben müssen. Das funktioniert nur dann, wenn ein Mutter-Taktgenerator und die notwendigen Frequenzteiler mehrere Tiefpassfilter steuern, die aber ebenso exakt der Frequenz des jeweiligen Rechtecksignales angepasst dimensioniert sein müssen. Je nach gestellter Aufgabe kann es durchaus Gründe geben den Weg der Schaltung in Bild 9 einzuschlagen. Wie ein solches Tiefpassfilter dimensioniert wird, ist nicht Gegenstand dieses Elektronik-Minikurses.
Vorbereitungen zum SC-Sinusgenerator
Wir verlassen an dieser Stelle die Anwendung eines zeitkontinuierlichen Tiefpassfilter zugunsten eines zeitdiskreten SC-Tiefpassfilter mit seinem typischen Vorteil der leichten Variation der Grenzfrequenz durch die Änderung der Taktfrequenz. Wer noch nicht weiss was ein SC-Filter ist, empfehle ich an dieser Stelle das Kapitel Linkliste. Man lese die angebotenen Elektronik-Minikurse über SC-Filter. Wichtig ist vor allem die Einführung. Am Schluss der Linkliste gelangt man per Mausklick wieder zurück hierher.
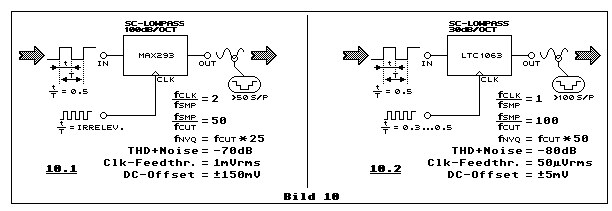
Wir beginnen mit einem Vergleich zwischen einem bereits bekannten
SC-Tiefpassfilter-IC, dem MAX293
(Elektronik-Minikurse 2 und 3)
von Maxim und LTC1063 von Linear-Technology
(LTC). Die Filtersteilheit (Dämpfungsverlauf im Sperrbereich) ist hier
nur insofern wichtig, dass sie die erste Oberwelle des Rechtecksignales
so stark dämft, dass die Sinusspannung einen für die Anwendung
genügend niedrigen Klirrfaktor aufweist. Dazu genügt der LTC1063, ein
SC-Tiefpassfilter 5. Ordnung. Mit 30 dB/Oktave ist er ausreichend, denn
die Signaldämpfung bei der ersten Oberwelle, bei der dreifachen
Grundfrequenz, beträgt 55 dB, wie Teilbild 8.2 illustriert. Das gilt,
wenn die Frequenz der eingangsseitigen Rechteckspannung identisch ist
mit der Grenzfrequenz des LTC1063.
In Bild 10 liest man für die Grenzfrequenz fCUT.
Dies heisst Cutoff-Frequency. Wie bereits zu Bilder 8 und 9 erläutert,
ist es oft besser, wenn die Filtergrenzfrequenz etwas höher ist als die
Frequenz des Rechtecksignals. Dadurch wird die Sinusspannung nur sehr
wenig gedämpft und deshalb bleibt die Amplitude der Sinusspannung, am
Ausgang des SC-Tiefpassfilters, wesentlich stabiler bei grosser
Frequenzänderung. Vorteile hat der LTC1063 eindeutig betreffs
Clock-Feedthrough-Spannung, DC-Offsetspannung, Klirrfaktor und Rauschen,
und dass die Taktfrequenz mit der Abtastfrequenz identisch ist. Das hat
zur Folge, dass die maximale Stufenzahl pro Sinusperiode 100 und nicht
nur 50 beträgt. Die Stufen entstehen durch die Abtastung. Diese
Stufenzahl von 100 ergibt sich, wenn die Sinusfrequenz der Grenzfrequenz
entspricht. Wählt man auf Grund der besseren Amplitudenstabilität eine
höhere Grenzfrequenz ist, bei gleicher Rechteck- und Sinusfrequenz, die
Anzahl der Stufen pro Periode proportional höher. Eine Glättung mit
nachgeschaltetem analogen Tiefpassfilter erübrigt sich oft. Eine
Kombination von SC- und Analog-Tiefpassfilter liest man in
(3). Dem Leser steht es frei gewisse Inhalte von
(3) mit den SC-Filter-Inhalten dieses
Elektronik-Minikurses zu kombinieren. Dies gelingt, wenn man genügend
Wissen und Erfahrung in der elektronischen Schaltungstechnik hat.
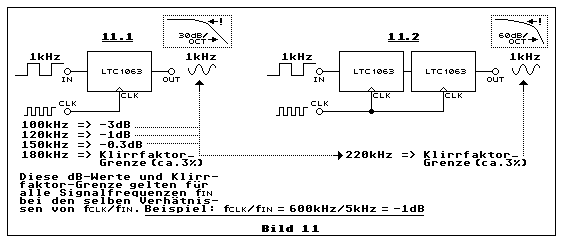
Teilbild 11.1 zeigt was es bringt, wenn man die Grenzfrequenz höher
wählt als die Frequenz des Rechtecksignales am Eingang. Bei einer
Taktfrequenz von 100 kHz beträgt die Grenzfrequenz 1 kHz. Grenz- und
Signalfrequenz sind identisch. Die Amplitudendämpfung beträgt 3 dB, so
wie es sein soll. Erhöhen wir die Taktfrequenz auf 120 kHz, reduziert
sich die Dämpfung auf 1 dB und bei 150 kHz sind es noch 0.3 dB. Diese
Dämpfungswerte gelten bei jeder andern Taktfrequenz innerhalb des
zulässigen Bereichs gemäss Datenblatt des LTC1063 und bei den selben
Frequenzverhältnissen. Wie wir bereits wissen, reduziert sich bei der
Erhöhung der Grenzfrequenz, in Relation zur Signalfrequenz, die
Dämpfung der Oberwellen, wobei besonders signifikant die erste, bei der
3-fachen Grundfrequenz, ist. Bei 180 kHz, also bei einer Grenzfrequenz
die mit 1.8 kHz fast doppelt so gross ist wie die Signalfrequenz von 1
kHz, zeigt sich auf dem Oszilliskopen bereits eine schwach wahrnehmbare
Sinusverzerrung, die etwa einem Klirrfaktor von 3 % entspricht.
Mit Teilbild 11.2 soll bloss gezeigt werden, um welchen Betrag die
Takt-, bzw. Grenzfrequenz in Relation zur Signalfrequenz weiter erhöht
werden darf, bis etwa das selbe Mass an Verzerrung des Sinussignales in
Erscheinung tritt. Anstatt 180 kHz sind es 220 kHz. Das zeigt, dass sich
der Zusatzaufwand eines zusätzlich zweiten SC-Filter-IC kaum lohnt.
Warum ist der Unterschied bei immerhin der doppelten Filtersteilheit von
60 dB/Oktave (10. Ordnung) statt 30 dB/Oktave (5. Ordnung) so gering?
Der Grund liegt im flacheren Verlauf der Dämpfung im Bereich der
Grenzfrequenz. Man beachte die Kurven bei den Grenzfrequenzen in den
beiden kleinen Diagrammen oberhalb der Sinus-Ausgangsspannungen in den
Teilbildern 11.1 und 11.2. Bei einem nichtkaskadierten echten
Tiefpassfilter ebenfals 10. Ordnung mit 60 dB/Okave, wäre das Resultat
besser. Man kann selbstverständlich den MAX293 mit 100 dB/Oktave
einsetzen, wobei man allerdings die andern Nachteile in Kauf nehmen
muss, wie dies in Bild 10 illustriert und im zugehörigen Text erklärt
ist.
Die genauen Angaben über Klirrfaktormesswerte fehlen, weil mir keine
Klirrfaktor-Messbrücke zur Verfügung stand. Das ist allerings für die
praktische Umsetzung dieser Inhalte kaum nötig, weil für hochpräzise
Sinus-Signalquellen, mit weit niedrigeren Klirrfaktoren, eignen sich
andere Methoden, wie die moderne DDS-Methode, besser. Man muss immer
auch daran denken, dass in der Region der Taktfrequenz (auch
Abtastfrequenz beim LTC1063) durch die Sinusstufen ebenfalls ein
Klirrfaktor bei hohen Frequenzen erzeugt wird, wobei dieser Anteil mit
zusätzlich analoger Tiefpassfilterung leicht unterdrückt werden kann.
Der SC-Sinusgenerator
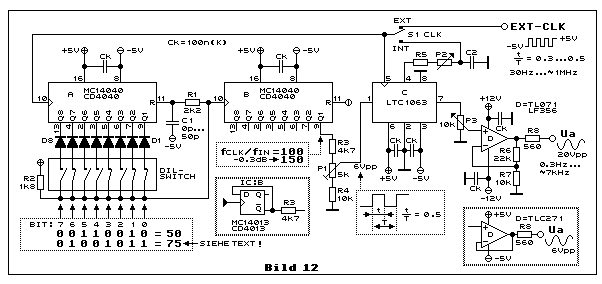
Wir beginnen schrittweise bei der Quelle mit dem Taktsignal und enden
beim Ausgang mit der Sinusspannung. Es gibt zwei Taktquellen, eine
externe am Eingang EXT-CLK und eine interne, welche das
SC-Tiefpassfilter LTC1063 (IC:C) beinhaltet. Dimensioniert wird dieser
interne Taktgenerator mit R5, P2 und C2. R5 verhindert, dass der Ausgang
(Pin 4) des Taktgenerators überlastet wird. R5 eignet sich aber auch,
um einen Frequenzbereich zu definieren. Um mehr zu erfahren, benutze man
die Informationen vom Datenblatt des LTC1063 im Kapitel
Self-Clocking-Operation.
Da die gesamte Schaltung, ausser Opamp IC:D, symmetrisch mit ±5 VDC
gespiesen wird, muss auch die Rechteckspannung des Taktsignales eine
symmetrische Spannung von annährungsweise ± 5 V (10 Vpp) aufweisen. Der
IC-interne Taktgenerator erzeugt diese symmetrische Taktspannung. An
EXT-CLK muss sie zugeführt werden. Steht nur ein externes Taktsignal
mit asymmetrischem Pegel (z.B. TTL-Pegel) zur Verfügung, muss dieses mit
einer zusätzlichen Schaltung in ein symmetrisches umgesetzt werden. Eine
solche zusätzliche Schaltung ist nicht Gegenstand dieses
Elektronik-Minikurses, aber man findet eine diskrete Methode mit zwei
Transistoren, eine mit einem mittelschnellen Komparator und eine
elegante etwas exotische Methode mit einem elektronischen analogen
Umschalter (Analog-Switch) im Elektronik-Minikurs
Vom Logikpegelwandler zum Impulsgenerator
in den Bildern 2, 5 und 6.
Vom Umschalter S1 führt das externe oder interne Taktsignal zum
Takteingang des SC-Tiefpassfilters IC:C (Pin 5) und zum Frequenzteiler
IC:A (Pin 10). IC:A arbeitet mit dem Diodennetzwerk D1 bis D8 und dem
8-poligen DIL-Schalter als einfacher programmierbarer asynchroner
Frequenzteiler. Ein DIL-Schalter genügt, weil der erwünschte
Teilungsfaktor in der Regel nur einmal oder wenige Male eingestellt
wird. Die Schalter von Bit 0, 1, 3 und 6 sind eingeschaltet skizziert.
Während des Hochzählens von IC:A bleibt immer mindestens einer der
eingeschalteten Bits auf LOW und damit auch der gemeinsame Anschluss
aller Schalter. Der Reseteingang R von IC:A liegt über R1 ebenfalls auf
LOW. Wenn die Dioden von Bit 0, 1, 3 und 6 auf HIGH schalten, hat IC:A
auf 75 gezählt. Der Pullupwiderstand R2 zieht den gemeinsamen Anschluss
aller Schalter und damit den Reseteingang von IC:A von LOW auf HIGH, was
vor dem folgenden Takt den Reset auslöst. Auf diese Weise teilt IC:A
die Taktfrequenz durch 75. Der kurze Resetimpuls, dessen Dauer durch die
sogenannten Propagation-Delaytimes von IC:A und der
R1C1-Verzögerungszeit bestimmt wird, taktet den nachfolgenden
Frequenzteiler IC:B, der jedoch, in der vorliegenden Anwendung, nur zur
Frequenzteilung 1:2 benötigt wird. Man könnte anstelle dieses MC14040
(CD4040) natürlich auch einen MC14013 (CD4013) (D-Flipflop) benutzen, -
siehe dickpunktierter Rahmen. Am Ausgang Q1 von IC:B steht ein
zeitsymmetrisches Rechtecksignal mit einer geteilten Taktfrequenz von
1/150 und einer Spannung von 10 Vpp zur Verfügung.
Mit dem Trimmer P1 stellt man den Wert auf etwa 6 Vpp ein. Damit wird
IC:C gerade noch nicht übersteuert. Das Verhältnis von der Taktfrequenz
zur Frequenz des Rechtecksignales am Signaleingang von IC:C (Pin 1) ist
mit 1/150 um einen Faktor 1.5 grösser als das Verhältnis von der
Taktfrequenz zur SC-Filter-Grenzfrequenz von 100. So wird wie
Sinusspannung am Ausgang von IC:C nur um etwa 0.3 dB gedämpft, was
sich, wie bereits bekannt, besonders günstig auf die
Amplitudenstabilität der Sinusspannung bei grosser Fequenzvariation
auswirkt. Mit dem DIL-Schalter kann man diesen Faktor zwischen mehr als
1.5 (< -0.3 dB und leicht höherer Klirrfaktor) und
1 (< -3 dB und niedrigster Klirrfaktor) wählen.
Mit P3 lässt sich die Sinusspannung Ua einstellen. Die Schaltung um IC:D
zeigt eine einfachte Verstärkerschaltung, um eine Sinusspannung von
maximal 20 Vpp (7 Vrms) zu erzeugen. Für IC:D ist dafür eine
Betriebsspannung von mindestens ±12 VDC, besser ±15 VDC, nötig. Genügt
jedoch eine Sinusspannung von 6 Vpp (2 Vrms), genügt auch für IC:D die
Betriebsspannung von ± 5VDC. Für IC:D eignet sich dann z.B. der TLC271,
der als Impedanzwandler mit Verstärkung 1 arbeitet, also R6 und R7
nicht benötigt. Eine Pufferschaltung mit einem Opamp am Ausgang von IC:D
sollte man auf jedenfall benutzen, weil man bei Direktanschluss von Ua
an IC:C, bei fehlerhafter Manipulation an Ua, die Zerstörung des
SC-Tiefpassfilters riskiert. Man sollte nicht auf die Idee kommen auf P3
zu verzichten und für die Spannungsvariation P1 vorziehen, weil dies
reduziert den Signal/Rausch-Abstand, wobei mit dem Rauschen
hauptsächlich die feinen Stufen der Sinusspannung und die Spannung des
Clock-Feedtrough gemeint ist.
Frequenzbereich der Sinusspannung Ua: Der Taktfrequenzbereich des
LTC1063 reicht von 30 Hz bis 4 MHz (bei Ub = ±5 VDC) und dies bedeutet
ein Bereich der Sinusfrequenz von 0.3 Hz bis 40 kHz. Die maximale
Frequenz des MC14040 beträgt minimal (Exemplarstreuung) 3.5 MHz (bei Ub
= ±5 VDC). Dies wird aber nicht erreicht, wenn durch Rückkopplung die
Frequenz geteilt wird. Im Datenblatt des MC14040 sind nur die
Verzögerungszeiten zwischen CLK nach Q1 (115 ns bis 230 ns) und CLK nach
Q12 (720 ns bis 1440 ns) angegeben. Bei der Resetauslösung werden die
Q-Ausgänge synchron zwischen 155 ns und 310 ns auf LOW gesetzt. Fazit:
Wenn man Pech hat mit den Daten von IC:A, liegt die maximale
Taktfrequenz unter 1 MHz. Mit einer Demoschaltung erreichte ich eine
maximale Taktfrequenz von 2 MHz, was einer maximalen Sinusfrequenz von
13.3 kHz entspricht. Das R1C1-Verzögerungsglied wird dann benötigt, wenn
die Daten günstig sind und eine relativ hohe Taktfrequenz möglich ist.
Dann muss die Impulsbreite für den Takteingang von IC:B evtl. leicht
vergrössert werden, z.B durch Variation von C1, damit IC:B sicher
arbeitet. Man kann R1C1 auch ganz weglassen, wenn die Daten ungünstiger
liegen und der Resetimpuls für den Takteingang des IC:B breit genug ist.
Dieser SC-Sinusgerenator eignet sich also eher für mittlere bis
niedrige, ja sogar für sehr niedrige Frequenzen.
Will man wesentlich höhere Sinus-Frequenzen erreichen, muss man für die
Frequenzteiler Highspeed-CMOS-Schaltungen, also den 74HC4040 (IC:A,B)
einsetzen. Da diese ICs aber mit maximal 6 VDC oder ±3 VDC betrieben
werden dürfen, muss auch der LTC1063 (IC:C) die selbe Betriebsspannung
erhalten, was durchaus erlaubt ist. Je nach maximaler Sinusspannung Ua
muss die Verstärkung von IC:D erhöht werden (R6/R7). Die Lösung für
einen schnelleren SC-Sinusgenerator überlasse ich dem
experimentierfreudigen Leser... :-)
Linkliste
Die folgenden Links bieten eine Einführung in die Methode der Filterung
mittels geschalteter Kapazitäten. Darum nennt man diese Art der Filter
Switched-Capacitor-Filter, abgekürzt SC-Filter. Dies im Gegensatz zum
zeitkontinuierlichen Filter aus Widerstand (Resistor) und Kondensator
(Capacitor), abgekürzt RC-Filter. Bei SC-Filtern übernehmen ein Schalter
und ein Kondensator die Funktion des Widerstandes. Genaugenommen müsste
man zwischen SCC- und RC-Filter unterscheiden, weil beim SC-Filter ein
Kondensator Teil des "simulierten" Widerstandes ist. Mehr dazu erfährt
man in der Einführung zum SC-Filter (1). Die
weiteren drei Links bieten praktische Anwendungen mit dem Einsatz von
käuflichen SC-Filter-ICs von Maxim und Linear-Technology:
- Das SC-Filter, kurze Einführung mit
praktischer Anwendung (1)
- SC-Tiefpassfilter-Einheit mit
umschaltbaren Grenzfrequenzen (2)
- Steuerbares und steiles Tiefpassfilter in SC-
und Analog-Technik (aktive RC-Filter) mit grossem
Frequenzbereich (3)
- 50-Hz-Notchfilterbank in
SC-Filter-Technik: PLL-Frequenzmultiplier (4)
- EMG-Testgenerator (Dreieckgenerator) (5)
- Zurück zum Anfang: Vorbereitungen zum SC-Sinusgenerator
Anhang
Die dB-Werte werden positiv (z.B. 3 dB) oder negativ (z.B. -3 dB) angegeben. Es geht dabei stets um Dämpfung. Wird das Wort Dämpfung mit Angabe des dB-Wertes erwähnt, enthält dieser dB-Wert kein Vorzeichen. Ohne Erwähnung des Wortes Dämpfung hat der dB-Wert ein negatives Vorzeichen, damit eindeutig die Dämpfung erkennbar ist. Dies sieht man so in den Bildern 7, 8 und 10 bis 12.