Dreieckgenerator mit Operationsverstärker


Wie kommt es zum Dreiecksignal?

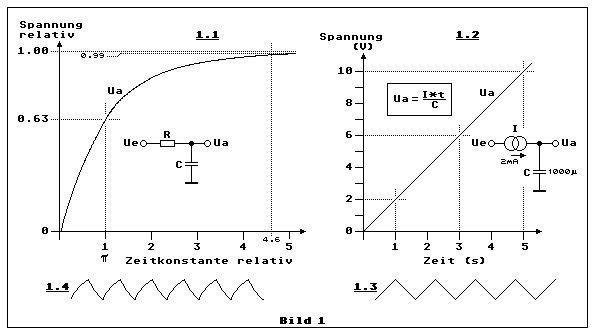
Wenn sich ein Kondensator C über einen Widerstand R auflädt, ergibt die Ladekurve die typische Exponentialfunktion, wie dies Teilbild 1.1 zeigt. Mit der Zeitkonstante τ erreicht die Spannung über C, hier Ua, einen Wert von etwa 0.63*Ue. Die Kurve flacht sich ab, weil der Strom, wegen der stetig abnehmenden Spannung über R, als wie kleiner wird. Nach etwa der 5-fachen Zeitkonstante approximiert Ua den Wert von Ue. Rein theoretisch erreicht Ua den Wert von Ue nie. Der selbe Vorgang gilt für die Entladung von C, wenn Ue nach dem Aufladen auf GND geschaltet wird. Nach der selben Zeitkonstante τ entladet sich C um den Spannungsfaktor von 0.63. Ua hat dann einen Wert von 0.37*Ue und nach etwa der 5-fachen Zeitkonstante approximiert sich Ua dem GND-Pegel. Diese inverse Funktion ist in Teilbild 1.1 nicht gezeichnet. Beides kommt dafür hier zum Ausdruck.

Da ein Dreieck aus Geraden besteht, ist eine Dreieck-Funktion mit einer RC-Schaltung nicht realisierbar. Jedoch eine IC-Schaltung macht dies möglich. IC bedeutet hier nicht Integrated-Circuit, sondern Strom-Kondensator! Bei einem konstanten Strom ändert sich die Spannung über C in Funktion der Zeit linear. Ist es eine konstante Stromquelle, steigt diese Spannung, ist es eine konstante Stromsenke, sinkt sie. Für Ladung und Entladung gilt die in Teilbild 1.2 angegebene Formel. Gezeigt wird auch gleich ein Beispiel mit I = 2 mA und C = 1000 µF. Mit diesen Werten steigt die Spannung Ua mit 2 V/s. In 5 s sind es 10 VDC, wie dies das Diagramm zeigt. Bei gleich grossem Entladungsstrom sinkt die Spannung Ua mit 2 V/s. Wechselt die Stromrichtung periodisch in gleichen Zeitabschnitten, entsteht eine Spannungsform von einer Serie von gleichschenkligen Dreiecken (Teilbild 1.3) und damit sind wir auch schon ein Schritt weiter auf dem Weg zum Dreieckgenerator. Würde nach dem selben Grundprinzip die Stromrichtung durch eine RC-Schaltung wechseln, entsteht ein Sägezahnbild (Teilbild 1.4). Die gekrümmten Linien sind nichts anderes als Ausschnitte der RC-Lade- und RC-Entladekurve (Ladekurve: Teilbild 1.1). Diese Ausschnitte entstehen, weil eine obere und untere Referenzspannung das Auf- und Entladen begrenzt und die Ladefunktion umschaltet. Die Spannung an C pendelt zwischen diesen beiden Spannungswerten. Bei der Erzeugung der Dreieickspannung ist es ebenso.

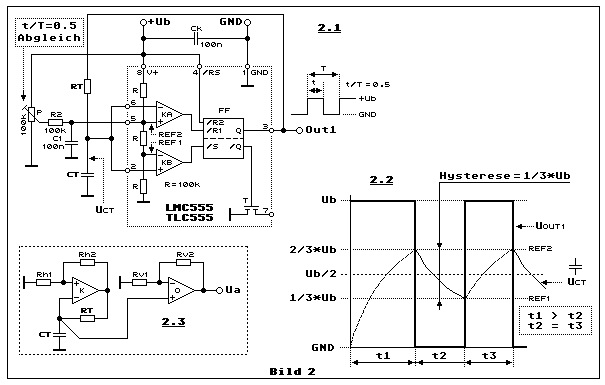
Aus Tradition zum Timer-IC 555 im ELKO-Forum, aber auch in meinen Elektronik-Minikursen, allerding fokussiert auf die CMOS-Version LMC555, soll hier untersucht werden, ob es mit diesem LMC555 möglich ist, einen Dreieckgenerator mit vertretbarem Aufwand zu realisieren. Teilbild 2.1 zeigt den typischen 555-CMOS:50%-Duty-Cycle-Generator in seiner Einfachheit, wie es nur mit der CMOS-Version des 555 möglich ist, weil für das Timing nur ein Widerstand RT und ein Kondensator CT benötigt wird. P und R2 sind nur dann nötig, wenn man das Tastverhältnis d/T exakt auf 0.5 abgleichen will. Die Schaltung beginnt ab R2, weil sie Teil aus Bild 2 des 555-CMOS: 50%-Duty-Cycle-Generator ist und dort ist R1 der Pullup-Widerstand an Pin 7 des LMC555, dessen Rechteckspannung z.B. für Synchronisierungszwecke benutzt werden kann.

Teilbild 2.2 zeigt die Rechteckspannung am Ausgang Out1 und die Spannungskurve am Timingkondensator CT die diese Rechteckspannung, begrenzt durch die Referenzspannungen REF1 und REF2, erzeugt. Beim Einschalten ist CT noch entladen. Die Ladung von CT über RT beginnt mit dem GND-Pegel und steigt bis REF2 weil Out1 auf dem HIGH-Pegel liegt. Dann setzt die Entladung von CT über RT ein, weil Out1 auf LOW umschaltet. Erreicht die Spannung an CT den Wert von REF1 schaltet Out1 wieder auf HIGH und das Ganze beginnt von Neuem. An CT entsteht eine typische symmetrische Sägezahnspannung aus den Fragmenten der Exponentialkurve. Man könnte mit einem Schmitt-Trigger mit sehr kleiner Spannungs-Hysterese (REF2-REF1) eine Gerade approximieren und durch nachträgliche Verstärkung eine approximierte Dreieckspannung erzeugen.

Teilbild 2.3 zeigt wie das geht, jedoch nicht mit dem LMC555. Komparator K arbeitet als Schmitt-Trigger mit einer sehr kleinen Hysterese. Wir betreiben diese Schaltung mit ±15 VDC, dann beträgt die Rechteckspannung am Ausgang von K etwa 26 Vpp. Mit Rh2 und Rh1 (h = Hysterese) legen wir eine Hysterese von 0.1 Vpp fest. Das bedeutet, Rh2 ist um den Faktor von 260 grösser als Rh1. Mit K und seiner Beschaltung haben wir den typischen Rechteckgenerator mit einem Komparator oder Operationsverstärker (Opamp) für niedrige Frequenzen. Nun verstärken wir die sehr kleine aber recht gut approximierte Dreieckspannung an CT mittels Opamp O auf z.B. 10 Vpp. Kein Problem mit einer Verstärkung von 100, gegeben mit Rv2/Rv1 = 100 (v = Verstärkung). Nachteilig bei dieser Methode ist eventuell die Rauschspannung, die durch die relativ hohe Verstärkung an O entsteht. Wenn man schon zwei aktive Komponenten benötigt, kann man diese auch so einsetzen, dass sie nicht isolierte einzelne Funktionen ausüben, sondern gemeinsam arbeiten und gleich von Anfang an eine Dreieckfunktion erzeugen. In beiden Methoden kann man für K auch einen Opamp einsetzen, wenn die Frequenz relativ niedrig ist.



Wenn's denn unbedingt ein 555er sein muss...

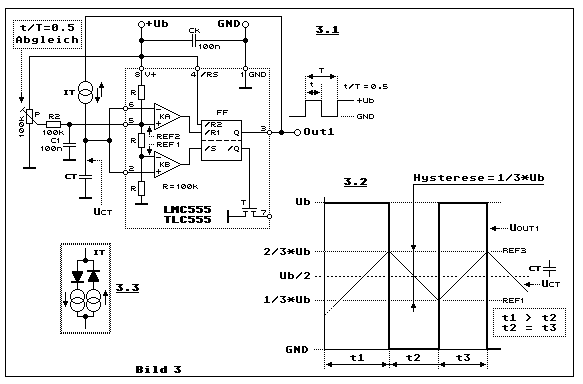
Nch dem kleinen Exkurs zur Methode mit Komparator oder Opmp in der Funktion als Schmitt-Trigger zur Erzeugung einer aus der Exponentialkurve approximierten Dreieckspannung, noch einmal zurück zum 555, um zu sehen was da sonst noch zu machen wäre in Richtung Dreieckspannung. Wir haben es auch hier mit einem, wenn auch ganz anders realisierten, Schmitt-Trigger zu tun. Mehr dazu liest man in (6) im Kapitel "Fensterkomparator + FlipFlop = Schmitt-Trigger". Da man mit Pin 5 nur den Zugang zu REF2 hat und kein weiterer Anschluss für REF1 zur Verfügung steht, ist es nicht möglich die Hysterese vernünftig zu beeinflussen. Sie ist daher mit 1/3*Ub vorgegeben. Eine vernünftige Dreieckapproximation aus der Exponentialkurve ist daher nicht realisierbar. Allerdings könnte man anstelle eines RC- ein IC-Glied (siehe Teilbild 1.2) einsetzen. Das Problem ist allerdings, dass diese Stromquelle IT (IT anstatt RT) bidirektional symmetrisch arbeiten muss. Das ist allerdings ziemlich aufwendig. Teilbild 3.3 zeigt nur eine prinzipielle Möglichkeit, die die Einfachheit auch nur vortäuscht. Man würde zwei komplementäre transistorisierte Konstantstromquellen (siehe Kapitel "Die Konstantstromzweipol-Methode") benötigen. Und dazu kommt, soll die Frequenz steuerbar sein, müssten beide Konstantstromquellen identisch gesteuert werden. Weitere Gedanken zu einer solchen Lösung erübrigen sich...



Im Endspurt zum Dreieckgenerator

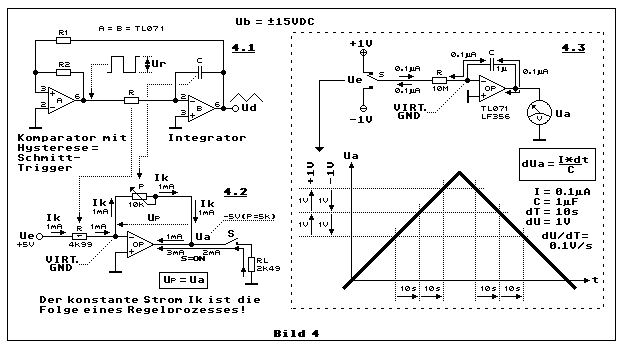
Wir nähern uns langsam dem bekannten Dreieckgenerator mit zwei Opamps (IC:A und IC:B) oder mit einem Komparator (IC:A) und einem Opamp (IC:B), je nachdem wie hoch die Frequenz der Dreieckspannung sein muss. Bei zu hoher Frequenz leidet die Flankensteilheit am Ausgang des IC:A, wenn ein Opamp statt ein Komparator (keine Frequenzgang-Kompensation) zum Einsatz kommt. Teilbild 4.1 zeigt die Einfachheit eines solchen Dreieckgenerators, der neben der Dreieckspannung Ud auch eine Rechteckspannung Ur erzeugt. Beide Signale sind voneinander abhängig. Wie aber funktioniert das? Der Komparator, der durch die Mitkopplung, gegeben aus R1 und R2, eine Hysterese bildet und als Schmitt-Trigger arbeitet, erzeugt aus der rückgekoppelten Dreieckspannung Ud vom Ausgang des Integrators zum nichtinvertierenden Eingang des Komparators (Schmitt-Trigger) (1) eine Rechteckspannung Ur, die ihrerseits mit Hilfe des Integrators die Dreieckspannung erzeugt...

Wir wissen aus Bild 3, dass eine Stromquelle mit einem konstanten Strom in einer bestimmten Zeit einen Kondensator laden und danach diesen mit einer Stromsenke mit dem selben konstanten Strom in der selben Zeit entladen muss, damit im Spannungs/Zeit-Diagramm ein gleichschenkliges Dreieck entsteht. Dies würde bedeuten, dass der Integrator mit IC:B (Bild 4) beide Funktionen aufweist: Er arbeitet als konstante Stromquelle und ebenso als konstante Stromsenke. Wobei das auch eine Angelegenheit der Definition ist. Wenn die Schaltung, wie hier in Bild 4, mit einer symmetrischen Betriebsspannung ±Ub arbeitet, kann man es ebenso gut als positive und negative Stromquelle bezeichnen, weil der Kondensator C abwechselnd auf eine positive und auf eine negative Spannung geladen wird. Bei einer einfachen Betriebsspannung mit +Ub ist es eindeutig. Da wird C geladen und entladen. Die symmetrische Betriebsspannung ±Ub erkennt man daran, dass sich die Referenzierung auf GND bezieht. Mit +Ub ist es oft +Ub/2. Jedenfalls ist es immer eine Spannung zwischen Ub und GND.

Wie es zum konstanten Stromfluss im Kondensator C in Teilbilbild 4.1 kommt, untersuchen wir mit Teilbild 4.2 mit einem dimensionierten Beispiel, das man experimentell nachvollziehen kann und auch sehr empfehlenswert ist! Hier hat es an Stelle des Kondensators C ein Potmeter P. Damit kann man sehr leicht nachvolziehen, dass der Strom bei variabler Spannung an P durch Veränderung des Widerstandes von P, konstant bleibt. Mit diesem Trick "simulieren" wir die veränderliche Ladespannung an C (Teilbild 4.1). Die Schaltung (Teilbild 4.2) zeigt nichts anderes als einen einfachen invertierenden Verstärker. Mit Potmeter P ist die Verstärkung einstellbar zwischen 0 und -2. Der konstante Strom am Eingang Ue ergibt sich durch die eingestellte Spannung von +5 VDC und dem Widerstand R mit 5 k-Ohm (1%-Reihe = 4k99). Der ebenfalls konstante virtuelle GND am invertierenden Eingang des Opamp sorgt für einen Strom von 1 mA, der den Weg von Ue über R und P zum Ausgang Ua des Opamp fliesst. Man verfolge den Weg des Stromes von 1 mA. Schalter S ist in diesem Experiment zunächst offen. Welche Spannung UP man auch einstellt, der Strom Ik = 1 mA bleibt konstant, solange die negative maximale Ausgangsspannung des Opamps an Ua nicht durch die negative Betriebsspannung -Ub begrenzt wird. Genau das selbe gilt, wenn anstelle der Änderung der Spannung über P sich die Ladespannung über C (Teilbild 4.1) sich ändert: Der Strom bleibt konstant!

Daran ändert sich auch nichts wenn man mit Schalter S eine Last RL dazuschaltet. Ist P z.B. auf den mittleren Wert von 5 k-Ohm eingestellt, beträgt die Verstärkung -1 und das bedeutet Ua = -5 VDC. Aus GND fliesst über RL mit einem Wert von 2.5 k-Ohm (1%-Reihe = 2k49) ein Strom von 2 mA zum Ausgang des Opamp Ua und dazu addiert sich der konstante Strom Ik von 1 mA zum Resultat von 3 mA. Dies soll einfach nur illustrieren, dass die Belastung am Ausgang des Opamps keinen Einfluss auf Ik hat und genau das gilt auch für Teilbild 4.1. Amplitude und Frequenz werden durch Änderung des Laststromes am Ausgang des Opamps nicht beeinflusst. Natürlich gilt auch hier, dass die Belastung den Opamp nicht überfordern darf. Das ist der statische Aspekt. Der dynamische ist, dass IC:A und IC:B eine wesentlich höhere Unity-Gain-Frequenzbandbreite haben müssen als die Frequenz der Dreieckspannung beträgt. Dabei ist die Slewrate, die auch abhängig von der Ausgangsspannung ist, nicht miteinbezogen.

Wie kommt es überhaupt zum konstanten Strom, der unabhängig ist von der Spannung über P (Teilbild 4.2) und über C (Teilbild 4.1)? Die typische Konstantstromquelle, wie sie in Bild 1 symbolisch angedeutet ist, besteht aus einer Referenzspannung die elektronisch in einen konstanten Strom umgesetzt wird, wie sie z.B. hier zum Ausdruck kommt. Da wirken die Basis-Emitter-Schwellenspannung (bip. Transistor) und die Gate-Source-Schwellenspannung (JFET) als ungefähre Spannungsreferenz, während hier eine hochpräzise Bandgap-Referenzspannung mit einem Opamp zum Einsatz kommen. Ganz anders funktioniert das hier beim Dreieckgenerator. Der konstante Strom kommt alleine durch die konstante virtuelle Spannung - hier virtueller GND - zustande. Der Widerstand R zwischen Ue und dem invertierenden Eingang beim Opamp (Teilbild 4.2) bestimmt bei gegebener Spannung Ue den konstanten Strom und dies ganz einfach deshalb, weil die virtuelle Spannung an diesem invertierenden Eingang konstant ist. Das ist aber alleine regeltechnisch definiert und funktioniert nur dann perfekt, wenn die geschlossene Schlaufenverstärkung (Closed-Loop-Gain) wesentlich niedriger ist als die interne Leerlaufverstärkung (Open-Loop-Gain) des Opamp. Und dies bedeutet, dass die Stromkonstanz in Funktion der Frequenz abnimmt, weil sich dadurch die Leerlaufverstärkung signifikant reduziert. Dies führt dann zwangsläufig zu einer Verzerrung der Dreieckspannung, weil dann der virtuelle GND am invertierenden Eingang ungenau wird. Auf den Punkt gebracht: Der konstante Strom Ik ist die Folge eines Regelprozesses.

Wir kommen jetzt zu Teilbild 4.3 mit ebenfalls einem selbst durchführbaren kleinen Experiment. Mit dem Schalter S spielen wir den Rechteckgenerator. Dabei schaltet man in einem selbstgewählten Rythmus um zwischen +1 VDC und -1 VDC. Weil wir hier beim manuellen Experiment ein langsames Ansteigen und Sinken der Ausgangsspannung Ua betrachten wollen, ist R = 10 M-Ohm und C = 1 µF. Man könnte auch 1 M-Ohm und 10 µF wählen. Das wäre jedoch für C problematisch, weil ein Kondensator mit 10 µF, der kein Elektrolytkondensator sein darf, schon recht gross und teuer ist. Es gibt zwei Gründe warum ein Elektrolytkondensator nicht taugt: Er ist polarisiert und hat zu hohe Eigenverluste.

Auch hier gilt, dass der invertierende Eingang ein virtueller GND ist. Das bedeutet, dass bei Ue = +1 VDC ein Strom von 0.1 µA vom Schalter S in Richtung invertierender Eingang und nach C fliesst und bei Ue = -1 VDC ein Strom von 0.1 µA vom C in Richtung invertierender Eingang und Schalter S fliesst. Dadurch ladet und entladet sich C, gemäss Formel, mit 0.1 V/s oder anders formuliert mit 1 V pro 10 Sekunden. Da kann man mit Schalter S und einer Stopuhr sehr leicht mit dem Lade- und Entladevorgang spielen und dabei das Voltmeter oder Multimeter (Spannungsanzeige) betrachten. Da R ziemlich hochohmig ist, sollte man als Opamp unbegingt ein Typ einsetzen, der JFET- oder MOSFET-Eingänge besitzt. Die empfohlenen TL071 oder LF356 haben JFET-Eingänge. Der Input-Bias-Strom beim TL071 beträgt typisch 65 pA und maximal 0.2 nA. Selbst für 1 nA wäre diese Versuchsschaltung, wo 100 nA fliessen, noch immer unproblematisch.

Was passiert eigentlich, wenn man den Schalter S in die spannungslose Mittelstellung setzen kann? Idealerweise würde die Spannung über C, die identisch ist mit Ua, konstant bleiben. Dem ist aber nicht so. Einerseits wirkt eine Selbstentladung von C über den eigenen extrem hochohmigen Innenwiderstand und über die ebenso hohen Widerstände zwischen den Anschlüssen auf einer sauberen Leiterplatte. Dazu kommt der erwähnte sehr schwache Input-Bias-Strom, der positiv oder negatv sein kann. Es kommt ganz drauf an was dominiert. Je nachdem ändert sich Ua ganz langsam in Richtung positive oder negative Maximalspannung.



Definitve Schaltungen im Einsatz

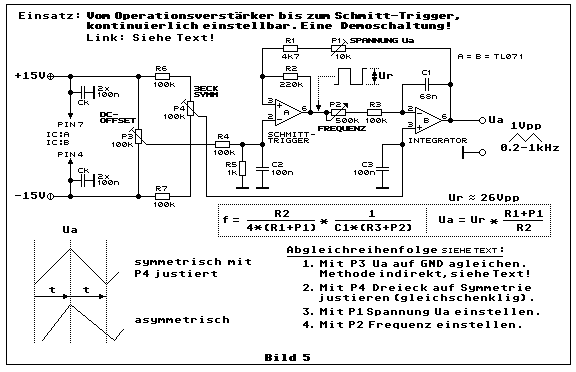
Die Schaltung des Dreieckgenerator in Bild 5 ist für den Elektronik-Minikurs (1) vorgesehen, sie ist aber ebenso universell einsetzbar. Das Funktionsprinzip ist bereits in Teilbild 4.1 erklärt.

Der Dreieckgenerator hier in Bild 5 besteht aus Erweiterungen, damit die Spannung (Potmeter P1) und die Frequenz (Potmeter P2) des Dreiecksignales einstellbar sind. Dazu kommt die Möglichkeit zur Justierung der DC-Offsetspannung mit P3 und der Abgleich der Dreiecksymmetrie mit P4.

Asymmetrisches Dreieck: Warum zeigt sich das Dreieck asymmetrisch, wenn die positiven und negativen maximalen Ausgangsspannungen von IC:A unterschiedlich sind? Die Ladezeiten von C1 sind unterschiedlich bei gleich grossen Ladeströmen. Dies lässt sich ausgleichen, wenn das Tastverhältnis der Rechteckspannung mit P4 in der Weise verändert wird, so dass die Ladedauer für den positiven und negativen Ladestrom für C1 gleich lang ist. Wenn z.B. die positive Spannungsaussteuerung am Ausgang von IC:A niedriger ist als die negative, ist die Ladezeit von C1 für den positiven Ladestrom geringer, wenn das Tastverhältnis von Ur zeitsymmetrisch t/T=0.5 ist. P4 ist dann nicht nötig, wenn die Aussteuerungs-Asymmetrie von IC:A nur sehr geringfügig ist. Das trifft bei der Verwendung des Opamp TL071 zu, wenn P2 und R3 nicht zu niederohmig sind, was hier der Fall ist. Verzichten kann man auf P4, wenn für IC:A ein Opamp oder Komaparator zum Einsatz kommt, der ausgangsseitig rail-to-rail-fähig ist. In diesem Fall kann man den nichtinvertierenden Eingang Pin 3 von IC:B direkt mit GND verbinden.

DC-Offsetspannung: Will man auf hohe Präzision verzichten, kann man diese Justierung weglassen und den invertierenden Eingang Pin 3 von IC:A direkt mit GND verbinden.

Für Präzisionsanwendungen lohnt sich jedoch der kleine Luxus der DC-Offset- und Dreieck-Symmetrie-Justierung und das trifft zu, wenn dieser Dreieckgenerator bei diesem Elektronik-Minikurs (1) zur Anwendung kommt. Übrigens, viele teure Funktionsgeneratoren haben diese Justierungsmöglichkeiten und man erkennt hier, wie einfach sie zu realisieren sind, wenn die Ansprüche nicht zu hoch sind.

Abgleichreihenfolge: Diese Reihenfolge ist in Bild 5 in vier Schritten beschrieben. Es beginnt mit (1.) dem Abgleich von Ua symmetrisch zum GND-Pegel. Das setzt aber voraus, dass an Ua die Dreieckspannung einigermassen symmetrisch mit P4 (2.) abgeglichen ist. Nun stellt sich die Frage, wie gleicht man denn an Ua die DC-Offsetspannung auf den GND-Pegel ab? Das geht nur indirekt in dem man die Dreieckspannung auf dem Bild des Oszilloskop exakt spannungssymmetrisch zum GND-Wert mit P3 justiert. Ist dies noch zuwenig präzis, kann man an Ua ein Multimeter anschliessen und auf den DC-Spannungsbereich einstellen. Ist die unverzerrte Dreieckspannung absolut symmetrisch zum GND-Pegel eingestellt, werden 0 VDC angezeigt. Danach kommt erst im zweiten Schritt mit P4 der exakte Abgleich der Dreiecksymmetrie.

Der nächste Schritt (3.) ist die Justierung der Dreieckspannung an Ua mit P1 und erst danach (4.) erfolgt die Einstellung der Frequenz mit P2. Warum diese Reihenfolge? Ganz einfach, die Variation der Dreieckspannung mit P1 variiert die Hysterese der Schmitt-Trigger-Schaltung mit IC:A und die Hysterese bestimmt die Umkehrtriggerspannungen, die identisch sind mit der Dreieckspannung (Vpp) an Ua. Je kleiner die Hysterese, um so kürzer sind die Ladezeiten von C1 und um so höher ist die Frequenz. Der konstante Ladestrom von C1 bleibt dadurch unverändert. Dieser wird nur durch die Variation von P2 beeinflusst.

Zweck der Dimensionierung dieses Dreieckgenerators ist die Anwendung mit diesem Elektronik-Minikurs (1) bei dem es darum geht die Eingenschaften des Opamp, Komparator und Schmitt-Trigger zu demonstrieren. Da braucht man eine fix eingestellte Dreieckspannung und eine variable Frequenz. Darum ist für P1 ein Trimmpoti und für P2 ein Poti gezeichnet. Will man einen preiswerten universellen Dreieckgenerator bauen, ist es selbstverständlich, dass die Einstellung der Dreieckspannung die Frequenz nicht beeinflussen darf. Deshalb muss die Spannungseinstellung nach dem Ausgang des Dreieckgenerator erfolgen, wie dies Bild 6 illustriert:

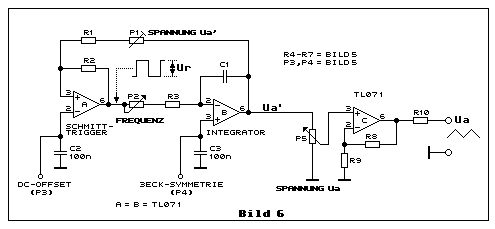
Dies geschieht mit P5 und dem darauffolgenden Opamp IC:C. Ob man mit R8/R9 verstärken will, ist davon abhängig ob Ua grösser sein muss als Ua', die Ausgangsspannung von IC:B. Falls keine Verstärkung nötig ist, können R8 und R9 entfallen und der Ausgang von IC:C wird direkt mit seinem invertierenden Engang verbunden. Dadurch hat man einen Impedanzwandler mit Verstärkung 1. Bei der Wahl des Opamp muss man darauf achten, dass er in diesem Fall unitygain-stable ist. R10 sorgt dafür, dass IC:C im Falle einer ausgangsseitigen kapazitiven Belastung (abgschirmtes Kabel) nicht zum Oszillieren neigt. Mit einem Wert von 560 Ohm trifft man als Ausgangswiderstand von etwa 600 Ohm für niederfrequente Anwendungen keine schlechte Wahl.

Es gibt noch eine elegantere Methode, die man als Lead-Kompensation bezeichnet. Da wird ein Widerstand in Serie zum Verstärkerausgang geschaltet, ohne dass sich die Ausgangsimpedanz erhöht und sogar eine wesentlich höhere (parasitäre) kapazitive Last am Ausgang zulässt, wenn nicht die Treiberfähigkeit der Ausgangsstufe darunter leidet. Mehr dazu erfährt man im Elektronik-Minikurs (9) im Kapitel "Die kapazitive Last am Ausgang des Opamp (Lead-Kompensation)" mit den beiden Bildern 9 und 10.



Einfacher Dreieckgenerator im Single-Supply-Betrieb

In diesem Elektronik-Minikurs (2) kommt ein kleiner und einfach realisierter Dreieckgenerator zum Einsatz. Hier wird erklärt wie er funktioniert:

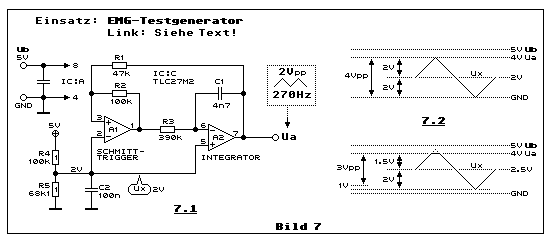
Dieser Dreieckgenerator ist in (2) batteriebetrieben. Eine 9-VDC-Blockbatterie speist einen Lowdropout-Spannungsregler mit einer Ausgangsspannung von 5 VDC. Diese Spannung speist den Dreieckgenerator mit IC:A. IC:A ist ein LinCMOS-Dual-Opamp. Was LinCMOS ist, liest man hier (10) im Kapitel "Der LinCMOS-Opamp". Es empfiehlt sich dieses Kapitel zu lesen, damit man diese Opamp-Familie ein wenig kennenlernt. Was wir hier wissen müssen, Ein- und Ausgang sind single-supply- jedoch nicht rail-to-rail-fähig. Die Common-Mode-Eingangsspannung reicht von GND bis 1V unterhalb der Betriebsspannung. Genau gleich beim Ausgang. Daher kann man die Ausgangsspannung nicht symmetrisch aussteuern, wenn man als Referenzspannung Ux die halbe Betriebsspannung Ub/2 einsetzt. Dies wäre dann der Fall, wenn R4 = R5.

Diagramm 7.2 zeigt die Ua-Aussteuergrenze von 4V und GND. Das bedeutet, dass eine Spannung an Ua maximal ein Peak-to-peak-Wert von 4Vpp haben kann. Das ist allerdings nur dann möglich, wenn die Arbeitspunktspannung Ux, nicht wie oft üblich, Ub/2 ist. Damit die Dreieckspannung bei Übersteuerung symmetrisch an ihren beiden Spitzenwerten begrenzt werden kann, muss die Spannung Ux genau halb so gross sein, wie die maximal mögliche Amplitude von 4 Vpp, also 2VDC anstatt 2.5 VDC (Ub/2). Dies erreicht man mit dem passenden Verhältnis von R4 zu R5. Ohne diese spezielle zu Ub asymmetrische Ux-Massnahme könnte man die Dreieckspannung nur bis auf 3 Vpp unverzerrt austeuern. Dies diktiert die maximale Aussteuerspannung von 4 V minus die halbe Betriebsspannung (Ub/2) von 2.5 VDC, multipliziert mit 2 (unteres Diagramm).



Links

Die ersten beiden Links haben direkt mit diesem Elektronik-Minikurs zu tun. Diese beiden Links sind ebenfalls Elektronik-Minikurse, die Dreieck-Signalspannungen benötigen. Die Schaltung des ersten kann sowohl mit einer Sinus- als auch mit einer Dreieckspannung auskommen, wobei sich das Dreiecksignal besser für die Demo eignet. Der zweite Elektronik-Minikurs enthält selbst einen Dreieckgenerator der hier thematisiert wird. Der dritte zum Thema Batterie-Indikator enthält auch ein Dreieckgenerator. Dabei wird die Referenzspannung und damit das Tastverhältnis so von der Batteriespannung gesteuert, dass sich zwischen geladen (grün), halbgeladen (gelb) und entladen (rot) die Farbe einer LED, ähnlich wie eines Regenbogen, ändert.