Gegentakt-Endstufe ohne Ruhestrom:
Die praktische und verzerrungsarme Anwendung
Einleitung
Für das Verständnis dieses anwendungsbezogenen Elektronik-Minikurses, ist das Studium des fundamentalen Voraussetzung. Hier der Link:
- Gegentakt-Endstufe ohne Ruhestrom: Theorie und Grundlage
Praktische Schaltung einer Audio-Endstufe ohne Ruhestrom
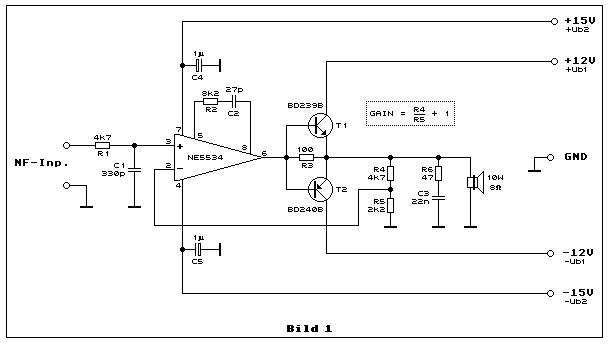
Anstelle des LF356, wie im
Theorieteil
thematisiert, wird hier ein
NE5534
verwendet. Dieser Opamp ist nicht weniger legendär. Er glänzt auch noch
heute vor allem im Audiobereich. Er hat eine niedrige äquivalente
Eingangs-Rauschspannungsdichte von 3.5 nV/sqrt(Hz) - geeignet z.B. als
Mikrophon-Vorverstärker für niederohmige dynamische Mikrophone oder
Elektret-Mikrofone - und er hat eine exzellente Treiberfähigkeit. Bei
einer Betriebsspannung von ±15 VDC kann der NE5534 eine Last von 600 Ohm
bis auf mindestens ±10 V ohne Amplitudenbegrenzung aussteuern. Gerade
diese Eigenschaft kommt der vorliegenden Anwendung zugute. Die
Unity-Gain-Bandbreite mit 10 MHz und die Slewrate von maximal 13 V/µs
des NE5534 sind gross genug. Die HIFI-Anforderungen werden in der
folgenden Anwendung mehr als erfüllt.
Dem aufmerksamen Leser fällt auf, dass in der Endstufe in Bild 1 R3
hinzugekommen ist. Einer dieser aufmerksamen Leser gab mir den Tipp ein
paar Worte dazu zuschreiben. Ich hole dies an dieser Stelle nach: Im
theoretischen Teil
fehlt R3 in Teilbild 4.2 absichtlich. Dieses Bild zeigt, wie die
Übernahmeverzerrung durch die starke Gegenkopplung praktisch
verschwindet. Es wird an dieser Stelle allerdings auch darauf
hingewiesen, dass die Unterdrückung der Übernahmeverzerrung
frequenzabhängig ist. Je schneller der Opamp die
Basis-Emitter-Schwellenspannungen der beiden Endstufentransistoren
durchlaufen kann, um so geringer wirkt sich die Übernahmeverzerrung bei
höheren Signalfrequenzen aus. R3 unterstützt den Opamp in dieser Arbeit.
Nämlich solange der Laststrom am Ausgang (Lautsprecher) sehr niedrig
ist, fliesst durch R3 der dazu notwendige Strom. Erst dann, wenn der
Laststrom soweit ansteigt - z.B. bei einer Sinusspannung -, dass der
Spannungsabfall an R3 die Basis-Emitter-Schwellenspannung einer der
beiden Endstufentransistoren (je nach Polarität) erreicht, fliesst in T1
oder T2 ein Basisstrom. Damit übernimmt der Transistor mit seinem
Emitterstrom jeden weiteren Stromanstieg. Der Strom in R3 bleibt
konstant, weil die Basis-Emitter-Spannung von T1 oder T2 bei diesem
Vorgang konstant bleibt. R3 ist nicht unwichtig, denn z.B. bei ganz
leiser Musik kann es sein, dass R3 zur Stromleitung einen erheblichen
Beitrag leistet und damit wird der Klirrfaktor zusätzlich unterdrückt.
Das passive Tiefpassfilter am NF-Eingang aus R1 und C1, mit seiner
Grenzfrequenz von etwa 100 kHz, verhindert die Einkopplung allfällig
hoher Feldstärken von AM-Radiosendern, falls die Zuleitung sehr lang ist
und als Empfangsantenne wirken könnte. In diesem Fall würde die
Eingangsstufe des Opamp als AM-Demodulator wirken und man hätte
unerwünschten Radioempfang. Meist sind es Kurzwellenseder. Der NE5534
ist intern frequenzgangkompensiert, jedoch nicht vollständig bis
hinunter zu sehr niedriger Verstärkung. Deshalb das zusätzliche
Kompensationsnetzwerk aus R2 und C2. Diese Verstärkerschaltung ist
erbrobt. Sie arbeitet in doppelter Ausführung (Stereo) seit Mitte der
1980er-Jahren in aktiven Küchenlautsprecherboxen, gesteuert von der
HIFI-Anlage aus meinem Wohnzimmer.
Warum zwei Betriebsspannungen?
Es gibt zwei unterschiedliche symmetrische Betriebsspannungen. Eine
stabilisierte elektronisch geregelte DC-Spannung von ±15 VDC für den
Opamp und eine unstabilisierte von etwa ±12 VDC für die Endstufe,
bestehend aus T1 und T2. Selbstverständlich könnte man auch diese
Endstufe mit der selben Spannung von ±15 VDC betreiben. Dies würde
jedoch eine unnötig höhere Verlustleistung an der Endstufe und an den
beiden Spannungsreglern (Bild 2) verursachen und einen
leistungsfähigeren Trafo voraussetzen (Bild 2). Es ist aber gar nicht
nötig die Endstufe mit einer stabilen, geregelten Spannung zu betreiben.
Die Spannungsregelung für die Lautsprecherspannung übernimmt ohnehin der
Opamp und die Referenz dazu ist die Eingangsspannung NF-Inp. Dazu kommt,
dass die ausgangsseitige maximale verzerrungsarme
Amplitudenaussteuerung, bei einer Betriebsspannung von ±15 VDC, bei
maximal ±12 V liegt. Dies deshalb, weil der Opamp selbst nur bis etwa 2
V unterhalb der positiven und negativen Betriebspannung gesteuert werden
kann und die Endstufentransistoren, als Emitterfolger arbeitend, die
maximale Aussteuerung noch einmal um etwa ±1 V oder etwas mehr
reduzieren.
Also darf die Betriebsspannung der Endstufe auf jedenfall niedriger
sein. Dass man für die ungeregelte Spannung ±12 VDC vorsieht ist
realistisch, weil dies wäre die Nennspannung, also dann wenn das
Netzteil (Bild 2) voll belastet ist. Dies ist aber bei
Audio-Endverstärkern nie der Fall. Realität ist, dass die mittlere
verbrauchte elektrische Leistung beim Lautsprecher sehr viel niedriger
ist und die Nennleistung meist nur in den Augenblicken von Bässen dann
herausgefordert wird, wenn beim Vorverstärker die Basseinstellung eine
starke Anhebung aufweist. Weil dem so ist, ist die ungeregelte
DC-Spannung von ±12 VDC durchschnittlich höher. Unbelastet liegt die
Sekundärspannung bei einem 25-VA-Trafo bis etwa 20% höher als bei der
Nennlast. Bei nur geringer Belastung liegt die Spannung für die Endstufe
bei etwa 13 bis 14 VDC. Mehr dazu im folgenden Abschnitt.
Netzteil zur (Stereo-)Audioendstufe von Bild 2
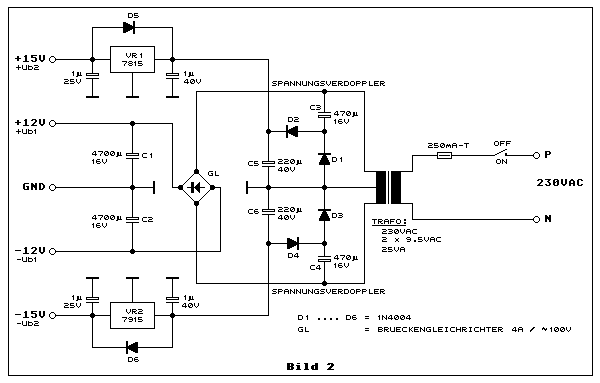
Dazu nehme man einen handelsüblichen Printtrafo mit einer Leistung von
25VA und einer doppelten Sekundärspannung von je 9 VAC oder 9.5 VAC, je
nachdem was man "von der Stange" bekommt. Für die Speisung von zwei
Endstufen (Stereobetrieb) gibt es eine simple ungeregelte duale
Brückengleichrichter-Elko-Speisung, bestehend aus GL, C1 und C2. Für die
geregelte Betriebsspannung von ±15 VDC mit den berühmten 7815 (VR1) und
7915 (VR2), braucht es eine symmetrisch aufgebaute Spannungsverdopplung,
bestehend aus D1 bis D4 und C3 bis C6.
Ein paar Worte zur Primärkreis-Sicherung von 250mA-T. T bedeutet träge.
Das sollte genügen, wenn man nicht einen Ringkerntrafo einsetzen will,
der höhere Einschaltstromspitzen aufweist. Dann wird man eine
doppelträge Sicherung mit der Bezeichnung 250mA-TT einsetzen müssen.
Eine Einschaltstrombegrenzung
ist bei solch niederiger Trafoleistung noch nicht nötig.
Warum eine symmetrische Speisung?
Warum braucht es denn eine symmetrische Speisung? Geht es denn nicht auch einfacher? So die Frage eines Leser. Meine Antwort: Das geht schon. Allerdings mit gewissen Nachteilen. Man betrachte dazu Bild 3:
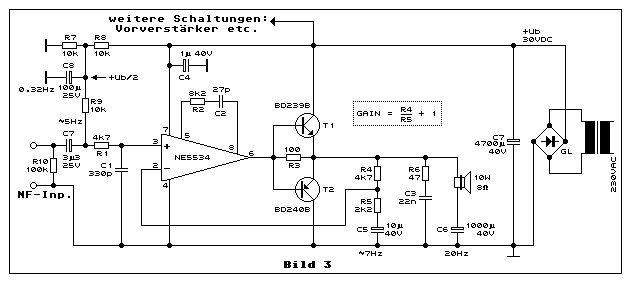
Geprüft habe ich diese Schaltung nicht, aber sie sollte funktionieren.
Anstelle eines GND als Arbeitspunkt, wie bei einer symmetrischen
Speisung, gibt es hier ein Arbeitspunkt, der in der halben
Betriebsspannung liegt. Messbar ist diese halbe Spannung +Ub/2 am Knoten
zwischen R7 und R8 (beide Widerstände gleich gross). Das Problem ist,
wie will man hier eine symmetrische Aufteilung der beiden
Betriebsspannungen für den Opamp-Teil und für die Transistor-Endstufe
realisieren? Geht nicht mit einfachen Mitteln. Man muss darauf
verzichten und so eine grössere Verlustleistung von T1 und T2 hinnehmen
oder man reduziert die Lautsprecherleistung mit einer niedrigeren
Betriebsspannung, z.B. mit +24 VDC, ebenfalls ungeregelt.
Ein paar Details. Der Parallelwiderstandswert von R7||R8 und die
Kapazität von C8 bilden ein passives Tiefpassfilter mit einer
Grenzfrequenz von 0.32 Hz. Bei einer Frequenz von 64 Hz wird die
Rippelspannung auf +Ub um den Faktor 200 (46 dB) gedämpft. Bei 100 Hz
ist es entsprechend etwas mehr. Es gilt bei einem Tiefpassfilter erster
Ordnung eine Asymptote von 20 dB pro Frequenzdekade. Eine Rippelspannung
von 1 Vpp (relativ starke Bassbelastung) reduziert sich auf weniger als
5 mVpp. Wobei das stimmt dann, wenn die Rippelspannung sinusförmig wäre.
Das ist natürlich nicht der Fall. Der Spannungsverlauf gleicht einem
Sägezahn mit einem starken Oberwellenanteil. Dieser Anteil liegt bei
wesentlich höheren Frequenzen und deshalb ist die Dämpfung etwas
grösser, bzw. die Rest-Rippelspannung an +Ub/2 niedriger.
Das passive Hochpassfilter aus C7 und R9 mit einer Grenzfrequenz von
etwa 5 Hz dient der DC-Entkopplung, damit am Eingang eine Audioquelle
mit Bezug auf GND angeschlossen werden kann. R10 ladet C7 auf +Ub/2.
Dies vermeidet ein lautes Knackgeräusch, wenn am Eingang im
Betriebszustand eine Audioquelle angeschlossen wird. Der eigentliche
Eingangswiderstand beträgt etwas weniger als 10 k-Ohm (Wert von R9),
weil der minimale Eingangswiderstand des NE5534 bei 30 k-Ohm (typisch
100 k-Ohm) liegt. C5 ist nötig, damit die Arbeitspannung +Ub/2 auch am
invertierenden Eingang (virtuelles +Ub/2) wirksam sein kann. Das passive
Hochpassfilter aus C5 und R5 hat eine Grenzfrequenz von etwa 7 Hz. Beim
Lautsprecher muss man die selben Vorkehrungen treffen mit C6. Ohne
diesen Elko würde durch den Lautsprecher ständig ein hoher DC-Strom
fliessen. Bei all diesen Massnahmen und Nachteilen, schätze ich die
Methode wie sie in Bild 1 und Bild 2 gezeigt wird. Viele professionelle
Audioanlagen arbeiten mit symmetrischen Betriebsspannungen.
Weitere Schaltungen, wie Vorverstärker und Klangeinsteller, sollte man
mit einer geregelten Spannung versorgen. Dazu eignet sich neben den
bekannten 78xx-Festspannungsregler hervorragend der LM317. Die
praktische Beschaltung und viele sinnvolle Hinweise zum LM317 erfährt
man in den folgenden zwei Elektronik-Minikursen:
- Integrierte fixe und einstellbare 3-pin-Spannungsregler
- Spannungsregler Spezial: Das 78xx-, LM317- und das Lowdropout-Prinzip
Lautstärke, Höhen, Bass und Balance
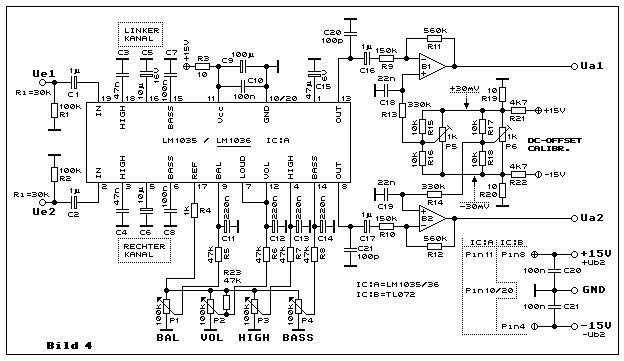
Ein Leser äusserte den Wunsch die Audioendstufe (Bild 1) mit einer
Klangregelschaltung in Stereoausführung zu erweitern. Nichts einfacher
als dies, denn genau so etwas habe ich damals für meine
Aktiv-Küchenlautsprecher realisiert. Ich musste mich allerdings erstmal
erkundigen, ob es das passende IC den LM1036 noch gibt. Der
LM1036 (Datenblatt)
ist nach wie vor erhältlich bei Farnell und Distrelec (März 2014).
Die Bauteilwerte um den LM1036 weichen teilweise von der
Application-Circiut auf Seite 5 des Datenblattes ab. Die Kapazitäten
C3,C4 mit 47 nF anstatt 10 nF für HIGH und C7,C8 mit 100 nF anstatt 390
nF für BASS entsprechen nicht den Originalwerten. Das kommt daher, dass
ich nicht das Diagramm "STANDARD APPLICATION CIRCUIT" (Figure 1) sondern
"INCREASED CONTROL RANGE" (Figure 3) realisiert habe. Siehe Seite 6 im
Datenblatt. Grund dafür sind die verwendeten preiswerten und relativ
kleinen Lautsprecher, welche nicht gerade mit einem linearen
Frequenzgang glänzen. So ist es trotzdem möglich, den Bassbereich mit
immerhin +17 dB ausreichend anzuheben. Für den Höhenbereich genügen
knapp mehr als +5 dB.
Für die Potmeter P1 bis P4 setzte ich 100 k-Ohm statt 47 k-Ohm ein. R23
mit 47 k-Ohm (wenn P2 = 100 k-Ohm) muss den "Todbereich" des
Volumereglers P2 zu reduzieren. Dies geht nicht aus dem Datenblatt
hervor. Mir fiel dies damals beim Experimentieren mit dem LM1035/36 auf
und handelte entsprechend. An den Ausgängen Pin 13 und Pin 8 zeigten
sich sehr hohe Oszillationsfrequenzen oberhalb von 100 MHz. Mit je einem
Keramikkondensator von 100 pF sind diese hohen Frequenzen
kurzgeschlossen oder beseitigt. R4 gibt es im Original nicht. R4 dient
als Kurzschlussschutz für die IC-interne Referenzspannungsquelle. Die
RC-Komponenten vor den IC-Eingängen VOL (Pin 12), HIGH (Pin 4) und BASS
(Pin 14) dienen der Dämpfung der Rauschspannung, die durch das Drehen
der Potmeter P1 bis P4 entsteht. Die Eingangsimpedanz liegt bei etwa 30
k-Ohm. Es empfiehlt sich daher auf jedenfall für beide Kanäle je einen
Impedanzwandler oder Verstärker vorzuschalten. Diese Massnahme schützt
auch den LM1036.
Es ist zu beachten, dass in der vorliegenden Anwendung der LM1036 nicht
symmetrisch gespiesen ist. Deshalb benötigt es an den Ein- und Ausgängen
DC-Entopplungsmassnahmen (C1,C2,C16,C17). Die Hochpass-Grenzfrequenzen
sind so gewählt, dass sie die untere Audiobandbreite nicht signifikant
reduzieren. C1*Ri = 5 Hz ; C16*R9 = 1 Hz. Das selbe gilt für den
rechten Kanal mit C2*Ri und C17*R10. In der Application Circuit im
Datenblatt auf Seite 5 wird als Blockapazität für die Speisung 10 nF
angegeben. Das ist definitiv so nicht brauchbar. Eine stabile und
brauchbare Lösung zeigte sich mit dem RC-Netzwerk aus R3, C9 und C10.
Die Betriebsspannung des LM1036 beträgt +9 VDC bis maximal +16 VDC. Hier
kommen stabilisierte +15 VDC (siehe Bild 2) zum Einsatz. Natürlich ist
es dem Leser freigestellt, die Schaltung so umzugestalten, dass ein
symmetrischer Betrieb für den LM1036 möglich ist. In diesem Fall gilt
ein Bereich für die Betriebsspannung von ±4.5 VDC bis maximal ±8 VDC.
Zur Anpassung an das Stereosignal einer Steuereinheit für die
Audioanlage, musste ich am Ausgang mit den Opamps IC:B1 und IC:B2 (ein
TL072) die Pegel um einen Betrag von etwa +12 dB (4x) verstärken. Diese
beiden Opamps dienen zusätzlich für den DC-Offset-Nullablgleich für die
beiden Audioendstufen (Bild 1), damit keiner der beiden Lautsprecher
auch nur einen geringen DC-Strom abkriegt. Wie man solche
Abgleichschaltungen im 10mV-Bereich elegant realisiert, erfährt man
in Operationsverstärker II.
Ein paar Worte zu Verlustleistung und Wärmeableitung
Die maximale Sinus-Leistung nimmt ein Lautsprecher dann auf, wenn die
Sinus-Spannung am Lautsprecher so hoch ist, dass diese in den
Amplitudenmaxima gerade noch noch nicht begrenzt wird. Bei der
vorliegenden Schaltung in Bild 2 sind das 7 Watt, wenn nur ein
Lautsprecher ausgesteuert wird. Arbeiten beide gleichzeitig unter der
selben Vollast, erreicht jeder einzelne Lautsprecher nur noch 6 Watt.
Beide zusammen 12 Watt. Im Einsatz ist ein Trafo der seine maximale
Leistung von 25 VA sekundärseitig abgibt.
Der Wirkungsgrad eines Klasse-B-Verstärker wird theoretisch mit bis zu
78% angegeben. Beim AB-Verstärker sind es 60 bis 70%. Mehr zum Thema der
unterschiedlichen Wirkungsgrade in Funktion der Verstärker-Klassen
erfährt man hier im ELKO-Schaltungstechnikkurs
Verstärker.
Alleine die Endstufe betrachtet, hat man es mit Klasse B zu tun. Es gibt
kein Ruhestrom, dafür jedoch die bekannte Übernahmeverzerrung. Liegt
diese Endstufe jedoch in der Gegenkopplungsschlaufe, wie dies Bild 1
illustriert, dann wirkt die gesamte Verstärkerschaltung wie Klasse AB.
Dabei stellt sich jetzt die Frage, hat diese Endstufe, wenn isoliert
betrachtet Klasse B ist, den selben Wirkungsgrad wie ein reiner
Klasse-B-Verstärker, mit bis zu 78%. Ich denke ja, ganz sicher bin ich
mir allerdings nicht. Um es genau zu nehmen, einen Ruhestrom gibt es
auch, nämlich den des Opamp NE5534 von maximal 8 mA (240 mW). Dazu kommt
noch, dass diese maximalen Wirkungsgrade nur dann zustande kommen, wenn
alle Komponenten genau auf einander abgestimmt sind. Und das scheitert
nur schon daran, wenn man einen Trafo "von der Stange" kauft...
Der langen Ausführungen kurzer Sinn, machen wir es einfach und sagen,
dass die Verlustleitung etwa gleich gross ist, wie die maximale
Sinus-Leistung an den beiden Lautsprechern und das sind ebenfalls etwa
12 Watt. Das ist ein durchaus realistischer Wert. Aber wir werden gleich
sehen, warum es gar nicht so drauf ankommt.
Diese Leistung muss in Form von Wärme mittels Kühlkörper von T1 und T2
abgeleitet werden. Stimmt das? Nein, stimmt nicht, ausser man
beabsichtigt einen totalen Gehörschaden zu riskieren, denn die
Mitteltonfrequenzen im kHz-Bereich sind bei solchen Leistungen an den
Lautsprechern extrem laut. Sanfte Musik mit Zimmerlautstärke benötigt
eine mittlere Leistung im unteren 100-mW-Bereich. Dies zum Vergleich.
Trotzdem, wie bereits angedeutet, benötigt man diese höhere Leistung zur
verzerrungsarmen Basswiedergabe. Die Taktdauer eines Bassereignisses in
Relation zur Taktperiode, z.B. durch eine Bassgitarre, ist relativ
gering, wodurch nur eine niedrige mittlere Bassleistung erfolgt. Deshalb
genügt eine Kühlkörper-Dimensionierung für beide Leistungsverstärker
gemeinsam von eindeutig weniger als 12 Watt. Trotzdem, wenn genug Platz
zur Verfügung steht, lohnt es sich stets die Kühlung grosszügig zu
dimensionieren, weil das kommt letztlich der Lebensdauer der ganzen
Schaltung zugute.
Es gibt ein Elektronik-Minikurs wo die Dimensionierung von Kühlkörpern
etwas thematisiert wird. Es gibt auch einen Online-Heatsink-Calculator.
Mehr dazu hier:
Technische Daten
Es gilt also, dass zwei Endverstärker (Bild 1) im Einsatz sind, welche vom Netzteil (Bild 2) gespiesen werden. Diese technischen Daten gelten ohne die Klangregelschaltung (Bild 4).
Verstärkung: 3.13 (10 dB) anpassungsfähig Maximale Sinus-Leistung: 7 W (nur ein Kanal im Einsatz) 6 W pro Kanal (beide Kanäle im Einsatz) (Last-Ersatzwiderstand zur Messung = 8 Ohm) Lautsprecheranforderung: je 10 Watt / 8 Ohm Leistungsbandbreite: 100 Hz bis 15 kHz (7W / 6W) 20 Hz bis 30 kHz (6W / 5W) Klirrfaktor bei je 4.5 Watt Sinusleistung an 8 Ohm: 0.23% bei 100 Hz 0.14% bei 1 kHz 0.06% bei 5 kHz 0.05% bei 10 kHz
Technische Daten im Visier...
Dem aufmerksamen Leser fällt bei den technischen Daten auf, dass die Frequenzbandbreite bei nur einem Watt weniger, drastisch besser ist. Die maximale Frequenz ergibt sich aus der Slewrate der gesamten Verstärkerschaltung. Oberhalb einer kritischen Frequenz und bei einer bestimmten Ausgangsspannung verzerrt sich der Sinus allmählich zu einem Dreieck. Wenn die Ausgangsspannung höher ist, setzt diese Verzerrung bei niedriger Frequenz ein. Mehr zum Thema Slew-Rate erfährt man hier:
- Operationsverstärker I
Warum verbessert sich noch drastischer die untere Grenzfrequenz von 100 Hz auf 20 Hz, wenn die Ausgangsleistung nicht auf die Spitze getrieben wird? Das kommt ganz einfach davon, wenn der Lautsprecherstrom bei sehr niedriger Audiofrequenz sehr hoch ist, dann interagiert der ebenfalls hohe Scheitelwert der Spannung am Lautsprecher mit der Rippelspannung an den Ladeelkos C1 und C2 (Bild 2) kritisch und komplex. Die Form der Rippelspannung wird durch Überlagerung des niederfrequenten Audiostromes verzerrt und vergrössert. Dies führt erst recht zum Klippen der Scheitelwerte der Lautsprecherspannung, wobei es auch zur Interferenz zwischen der niedrigen Audiofrequenz und der 100-Hz-Frequenz der Rippelspannung an den Ladelkos kommt. Bei höheren Audiofrequenzen bei grosser Belastung, ist die Rippelspannung an den Ladeelkos niedriger, weil die schnelleren Laststromänderungen durch die Ladeelkos besser integriert (ausgemittelt) werden.
Das Boucherot-Glied
Erster Leserbeitrag von Christian Heiling (Infineon)
Ich möchte Dir einen kleinen Nachtrag zu Deinem Elektronik-Minikurs mit
dem Titel Gegentakt-Endstufe ohne Ruhestrom: Die praktische und
verzerrungsarme Anwendung vorschlagen. Darin ist nämlich das, meiner
Meinung nach nicht ganz unwesentliche, R-C-Glied - bestehend aus R6 (47
Ohm) und C3 (22nF) - nicht dokumentiert.
Es handelt sich dabei um ein sogenanntes Boucherot-Glied, das
seinen Namen dem gleichnamigen französischen Schaltungstechniker
verdankt. Grundsätzlich dient es zu einer Art "Blindstromkompensation"
indem es die positive Reaktanz, die in der Lautsprecherimpedanz
(=induktiver Anteil) enthalten ist, durch die negative Reaktanz des
RC-Gliedes kompensiert und damit einen reellen Abschluss der
Verstärkerstufe erzeugt.
Nachdem diese Art der Kompensation natürlich immer nur für eine einzige
Frequenz gültig ist, in einem Audiosignal aber immer ein
Frequenzspektrum vorliegt, gibt es kaum einen nachvollziehbaren
mathematischen Hintergrund für die Dimensionierung des Boucherotgliedes.
Vielmehr verlässt man sich dabei auf empirisch ermittelte
Erfahrungswerte, wie es auch hier der Fall zu sein scheint.
Typische Werte der Elemente liegen für R zwischen 10 und 100 Ohm und
für C zwischen 10 und 100 nF. Diese Werte liefern eben für gängige
Lautsprechertypen im Bereich der statistisch maximalen Lastverteilung
gute Ergebnisse. Für qualitative sehr hochwertige Systeme werden
ohnehin Mehrweglautsprechersysteme verwendet, bei denen man die
Frequenzbereiche der einzelnen Lautsprecher enger eingrenzen kann als
es hier möglich ist.
Noch ein Hinweis für den Bastler:
Wenn die Verstärkerstufe z.B. zur Messung der (Leistungs)Bandbreite nahe
der oberen Grenzfrequenz (oder gar darüber - falls jemand nur die
Endstufe alleine testen möchte und Vorverstärker und Begrenzerfilter
weglässt) mit voller Amplitude betrieben wird, ist der kapazitive
Widerstand (hier von C3) relativ gering und es kann unter Umständen
vorkommen, dass der ohmsche Widerstand (hier R6) thermisch überlastet
wird und "abbrennt". In diesem - im normalen Betriebszustand nicht
auftretenden Sonderfall - ist die leistungsmässige Dimensionierung des
vorliegenden Boucherotgliedes zu beachten, wenn man dichten Qualm im
Labor vermeiden möchte.
Das Boucherot-Glied
Zweiter Leserbeitrag von Christian Heiling (Infineon)
Dieser zusätzlicher Leserbeitrag von Christian Heiling (bezieht sich auf
eine frühere Diskussion in den folgenden anklickbaren Newsgruppen des
UseNet und Mausnet).
In denen von Dir angegebenen Diskussionsforen...
- de.sci.electronics (UseNet)
- maus.technik.elektronik (Mausnet)
...habe ich die Beiträge gelesen und bin zum Schluss gekommen, dass es
dort Leser gibt, die sich mit dem mathematischen Hintergrund des
Boucherotgliedes beschäftigen möchten. Aus diesem Grund ein weiterer
Nachtrag meinerseits:
Grundsätzlich werden 2 Behauptungen aufgestellt:
1. Ist man der Meinung, dass das Boucherotglied zur Unterdrückung
von hochfrequenten Ausgangsspannungen dient. Das ist im allgemeinen zwar
nicht sehr weit von der Wahrheit entfernt, trifft im konkreten Fall der
Gegentaktendstufe aber eher weniger zu. Die Sache ist nämlich die: Die
Ausgangsimpedanz der Endstufe ist sehr niedrig und so macht es kaum
Sinn, Hochfrequenzen gegen Masse abzuleiten. Viel mehr muss man hier
eine frequenzabhängige Gegenkopplung einsetzen, die Hochfrequenzen am
Ausgang erst gar nicht entstehen lässt, weil diese schon eingangsseitig
unterdrückt werden.
(In der im Elektronik-Minikurs angegebenen Schaltung ist das nicht
wirklich erfolgt. Das eingangsseitige Tiefpassfilter und die zusätzliche
Frequenzgangkompensation reichen aber völlig aus.)
Tatsächlich kann man das Boucherotglied zu diesem Zweck verwenden, wenn
keine Gegentaktendstufe vorliegt und z.B. direkt der Ausgang des OpAmp
verwendet wird (z.B. für Kopfhörer). Dann macht es durchaus Sinn die
Gegenkopplung durch starke Ausgangsbelastung abzuschwächen. Besonders
geeignet sind dazu aber Verstärkerschaltungen die mit einem
2. Bernd Mayer behauptet, dass man die Kapazität im
Boucherotglied gemäss der Gesetzmässigkeit C=L/(R*R) allgemein
bestimmen kann. Das ist unter einer Bedingung völlig richtig! Diese
Bedingung ist - Bernd hat richtigerweise auch das korrekt erwähnt - dass
die beiden ohmschen Anteile gleich gross sein müssen.
Warum das so ist?
Nicht ganz einfach zu berechnen, aber doch leicht zu verstehen!
Es liegt also eine Parallelschaltung aus einem RC und einem RL Glied vor,
wobei R in beiden Fällen gleich ist.
Berechnung der Resonanzfrequenz:
Man berechne: (R + 1/(j*w*C))||(R + j*w*L) --> die
Resonanzbedingung ist, dass der Imaginärteil gleich Null ist. Setzt
man also ....*j = 0 und löst die entstehende Gleichung nach
w auf, kommt man zum bekannten Ergebnis w = sqrt(1/(L*C)).
Löst man die Gleichung aber nicht nach w, sondern nach C,
so wird man feststellen, dass sich w eliminiert und man die
frequenzunabhängige Bedingung C=L/(R*R)erhält. Setzt man C diesen
Wert, so ist die Last für alle Frequenzen gleich R (Idealfall).
Wie kann das sein? - es lässt sich auch logisch erklären:
Bei steigender Frequenz erhöht sich die Reaktanz der Induktivität L gemäss
XL=j*w*L - dafür sinkt der sie durchfliessende Strom iL -
womit die Spannung uL=iL*XL konstant bleibt.
An der Kapazität herrschen analoge Verhältnisse. Der interessierte
Leser kann sich das anhand eines Zeigerdiagrammes visuell vor Augen
führen und wird die "totale Kompensation" mit Sicherheit verstehen.
Die Dimensionierung von C mit Hilfe einer Messung der Sprungantwort der
Lastimpedanz plus Boucherotglied ist eine gute Idee. Man kann auch - wenn
man eine beliebig grosse, genaue Referenzkapaziät verwendet und so die
Resonanzfrequenz ermittelt, die Induktivität L einigermassen schnell und
ausreichend genau bestimmen!
Somit verbleibt mir, dem Leser für sein Interesse zu danken, und für
weitere Fragen zu Verfügung zu stehen.
MfG. Christian